Комбинаторика
Комбинаторика – раздел математики, занимающийся изучением количества возможных комбинаций определенного типа, которые возможно сделать из некоторого набора элементов. Эти вычисления необходимы для решения различных задач в теории вероятностей и получения распределений случайных величин.
Правила в комбинаторике
Правило суммы: если есть взаимоисключающие друг друга действия A и B, которые можно выполнить способами m и n соответственно, то выполнить любое из этих действий можно m + n способами.
Правило произведения: если есть последовательность действий k, и первое действие его можно выполнить n1 способом, второе n2 и далее до nk, то все действия этой последовательности можно выполнить n1 · n2 · nk способами.
Элементы комбинаторики
Размещения из n по k – упорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Для расчета способов размещения следует воспользоваться формулой: Pkn = n! / (n - k)!
Перестановки – конечное множество, в котором указан порядок его элементов. Количество перестановок вычисляется по формуле: Pn = n!
Сочетания из n по k – неупорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Число сочетаний из n элементов по k рассчитывается так: n! / (n - k)! · k!
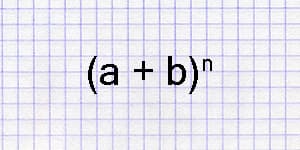
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
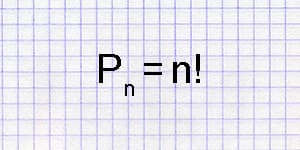
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
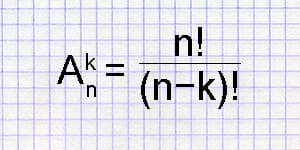
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
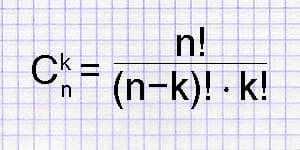
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.