Калькулятор числа перестановок
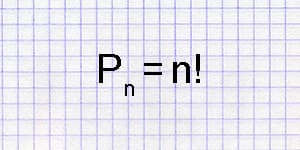
Число перестановок - это количество различных способов упорядочить n различных объектов. Например, число перестановок 3 объектов равно 6, поскольку существует 6 различных способов упорядочить 3 объекта:
| 1 | 2 | 3 |
| 1 | 3 | 2 |
| 2 | 1 | 3 |
| 2 | 3 | 1 |
| 3 | 1 | 2 |
| 3 | 2 | 1 |
Формула для расчета числа перестановок n объектов:
n! = n * (n - 1) * (n - 2) * ... * 1
где n! означает факториал n.
Например, число перестановок 5 объектов равно 120, поскольку:
5! = 5 * 4 * 3 * 2 * 1 = 120
Число перестановок используется во многих областях математики, включая комбинаторику, теорию вероятностей и статистику.
Примеры использования числа перестановок
В комбинаторике число перестановок используется для подсчета количества различных способов выбора и упорядочивания элементов из множества. Например, число перестановок 5 элементов, из которых 2 одинаковы, равно 60, поскольку существует 60 различных способов выбрать 2 элемента из 5 и упорядочить их.
В теории вероятностей число перестановок используется для подсчета вероятности того, что n объектов будут упорядочены в определенном порядке. Например, вероятность того, что 5 монет упадут на стол в порядке HTTH, равна 1/60, поскольку существует 60 различных способов упорядочить 5 монет, и только один из них соответствует порядку HTTH.
В статистике число перестановок используется для подсчета количества различных результатов, которые могут быть получены в результате эксперимента. Например, если из колоды карт наугад выбирается 5 карт, то число возможных результатов равно 2520, поскольку существует 2520 различных способов выбрать 5 карт из 52.
Дополнительные сведения
Число перестановок можно также рассчитать с помощью рекуррентного соотношения:
P(n) = n * P(n - 1)
где P(n) означает число перестановок n объектов.
Число перестановок является специальным случаем числа сочетаний, которое используется для подсчета количества различных способов выбрать k элементов из множества n элементов.
Комментарии к калькулятору
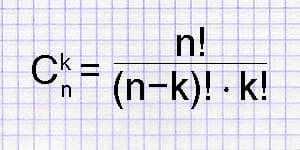
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Перейти к расчету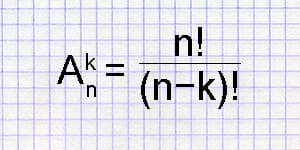
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
Перейти к расчету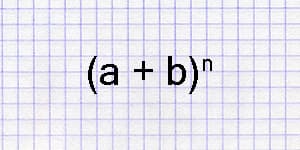
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
Перейти к расчету
Это называется факториал. Или можно сказать, что это произведение чисел от 1 до n.
А что значит восклицательный знак вот тут: "n!"?