Калькулятор числа размещений
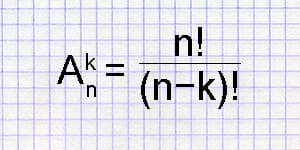
Число размещений - это важное понятие в комбинаторике и теории вероятностей, описывающее упорядоченные комбинации элементов. Будь то решение математических задач, работа с вероятностью или изучение алгоритмов, понимание числа размещений имеет ключевое значение.
Что такое число размещений?
Размещением называется упорядоченное распределение различных элементов. Порядок элементов имеет значение, что означает, что изменение порядка приводит к другому размещению. Для набора из \(n\) различных элементов число размещений обозначается \(n!\), читается как "n факториал".
Функция факториала определяется как произведение всех положительных целых чисел до заданного числа. Математически это выглядит следующим образом:
\[ n! = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1 \]
Расчет числа размещений
Существует несколько сценариев, в которых рассчитываются размещения, в зависимости от ограничений и требований задачи. Вот несколько общих случаев:
Размещения без повторений
При упорядоченном распределении \(k\) элементов из множества \(n\) различных элементов без повторений число размещений задается формулой:
\[ A(n, k) = \frac{n!}{(n-k)!} \]
Размещения с повторениями
Когда некоторые элементы повторяются в множестве, формула для размещений с повторениями выглядит так:
\[ A(n; n_1, n_2, \ldots, n_k) = \frac{n!}{n_1! \cdot n_2! \cdot \ldots \cdot n_k!} \]
где \(n_1, n_2, \ldots, n_k\) - это количество повторов каждого различного элемента.
Применение числа размещений
Понимание числа размещений находит применение в различных областях. Некоторые примеры включают:
- Криптография: Размещения играют важную роль в создании безопасных алгоритмов шифрования.
- Вероятность: Расчет размещений необходим для определения возможных исходов в вероятностных экспериментах.
- Проектирование Алгоритмов: Размещения являются фундаментальными при проектировании алгоритмов для поиска, сортировки и оптимизации.
- Теория игр: Размещения используются для анализа и стратегии в играх и сценариях принятия решений.
Число размещений - это фундаментальное понятие с широким спектром применения в математике и за её пределами. Будь то изучение элегантности комбинаторики или решение реальных проблем, твердое понимание числа размещений - это ценный ресурс. Погружаясь в мир размещений, вы раскроете их красоту и универсальность в решении разнообразных задач.
Комментарии к калькулятору
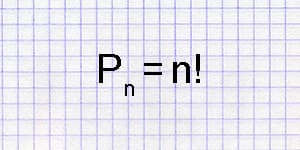
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчету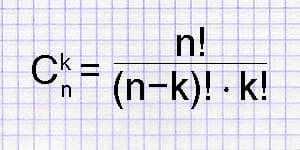
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Перейти к расчету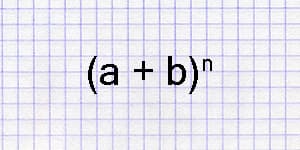
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
Перейти к расчету
Кто-нибудь может вообще нормально объяснить, что такое эти размещения?