Объем усеченной пирамиды
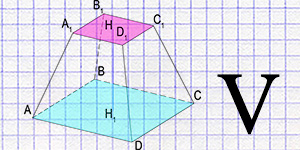
Усеченная пирамида представляет собой уникальную геометрическую фигуру, полученную путем пересечения обычной пирамиды плоскостью, параллельной ее основанию. В результате такого пересечения верхняя часть пирамиды отсекается, оставляя фигуру с двумя параллельными основаниями различного размера. Усеченные пирамиды можно встретить во многих архитектурных сооружениях, от древних пирамид до современных зданий. Эта фигура играет важную роль не только в архитектуре, но и в многих других областях, включая математику, физику и инженерию.
Исторически усеченные пирамиды использовались во многих культурах по всему миру. Они служили не только практическим целям в строительстве, но и часто имели символическое или религиозное значение. В архитектуре древних цивилизаций усеченные пирамиды могли обозначать места поклонения или могильные комплексы.
С математической точки зрения, усеченная пирамида представляет собой интересный объект из-за своих свойств и вариаций формы. Понимание того, как рассчитать объем такой фигуры, имеет важное значение во многих практических и теоретических приложениях. Это знание полезно не только для профессионалов, занимающихся строительством и дизайном, но и для студентов, изучающих основы геометрии.
Геометрическое описание
Усеченная пирамида является многогранником, который образуется в результате пересечения правильной пирамиды плоскостью, параллельной ее основанию. Она характеризуется рядом геометрических свойств:
- Усеченная пирамида имеет два основания - верхнее и нижнее. Оба основания являются параллельными друг другу и могут быть любыми многоугольниками одинаковой формы, но разного размера.
- Боковые грани усеченной пирамиды - это трапеции. Их количество равно количеству сторон основания.
- Высота усеченной пирамиды (h) - это перпендикуляр, опущенный от верхнего основания к нижнему.
- Апофема - это высота боковой трапециевидной грани, проведенная от вершины до середины стороны основания (только для правильных усеченных пирамид).
Таблица характеристик усеченной пирамиды
| Характеристика | Описание |
|---|---|
| Основания | Два параллельных многоугольника |
| Боковые грани | Трапеции |
| Высота | Перпендикулярное расстояние между основаниями |
| Апофема | Высота боковой грани (для правильной усеченной пирамиды) |
Математические формулы
Площадь основания (S) зависит от формы основания. Для правильного многоугольника можно использовать формулу \( S = \frac{n \times a^2}{4 \times \tan(\frac{\pi}{n})} \), где n - количество сторон, a - длина стороны.
Математическая формула для расчета объема усеченной пирамиды основывается на площадях ее верхнего и нижнего оснований, а также на ее высоте. Формула для вычисления объема V усеченной пирамиды задается как:
где:
- S_1 и S_2 - площади верхнего и нижнего оснований соответственно,
- h - высота усеченной пирамиды, измеренная как перпендикулярное расстояние между двумя основаниями.
Пример расчета объема
Рассмотрим усеченную пирамиду с квадратными основаниями, где сторона нижнего основания a_1 = 6 м, сторона верхнего основания a_2 = 4 м, и высота h = 5 м.
- Площадь нижнего основания S_1 = a_1^2 = 6^2 = 36 \, м^2
- Площадь верхнего основания S_2 = a_2^2 = 4^2 = 16 \, м^2
- Объем усеченной пирамиды: V = \frac{1}{3} \times 5 \times (36 + 16 + \sqrt{36 \times 16}) \asymp 141.67 \, м^3
Таким образом, объем данной усеченной пирамиды составляет приблизительно 141.67 кубических метров.
Заключение
Усеченная пирамида представляет собой уникальную геометрическую фигуру, обладающую интересными свойствами и широким спектром применения. Расчет объема усеченной пирамиды - важный навык в геометрии, архитектуре и инженерии. Понимание принципов, лежащих в основе этих расчетов, помогает глубже осмыслить пространственные структуры и их взаимосвязи.
Список литературы и ресурсы
- Стюарт, Джеймс. "Калькулюс". Cengage Learning, 2015.
- Липсон, Стивен Г. "Стереометрия: Понимание трехмерной геометрии". Dover Publications, 2016.
- Александров, А.Д. "Геометрия". Москва: Наука, 1989.
- Weisstein, Eric W. "MathWorld - A Wolfram Web Resource".
- "Khan Academy - Geometry".
Комментарии к калькулятору

Калькулятор расчета объема пирамиды через высоту и площадь основания или одну из сторон основания.
Перейти к расчету
Расчет объема усеченного конуса через радиус/диаметр нижнего и верхнего основания и высоту.
Перейти к расчету
Нахождение объема тетраэдра через длины ребер, радиусы списанной и описанной окружностей.
Перейти к расчету