Объем усеченного конуса
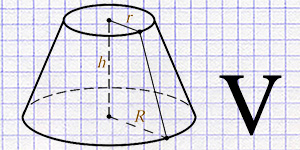
Усеченный конус является одной из базовых и важных геометрических фигур в математике и физике. Эта фигура представляет собой конус, верхняя часть которого отсечена плоскостью, параллельной основанию. Усеченный конус характеризуется двумя круглыми основаниями разного диаметра и боковой поверхностью, образованной образующими, соединяющими соответствующие точки на этих основаниях.
Исторически усеченные конусы нашли широкое применение в архитектуре и инженерии. Они используются в конструкциях многих архитектурных сооружений, от древних храмов до современных зданий. Усеченные конусы также применяются в различных областях техники, например, в дизайне турбин или вентиляционных систем.
Геометрическое описание усеченного конуса
Усеченный конус представляет собой трехмерную геометрическую фигуру, полученную путем пересечения правильного конуса плоскостью, параллельной его основанию. Геометрические свойства усеченного конуса включают:
- Основания: два круглых основания разных диаметров, расположенных параллельно друг другу.
- Боковая поверхность: наклонная поверхность, образованная образующими, соединяющими края оснований.
- Высота (h): перпендикулярное расстояние между основаниями.
- Радиусы оснований (R и r): радиус большего и меньшего оснований соответственно.
- Образующая (l): расстояние от края одного основания до края другого, проходящее по боковой поверхности.
Таблица характеристик усеченного конуса:
| Характеристика | Описание |
|---|---|
| Основания | Два параллельных круга разного радиуса |
| Боковая поверхность | Наклонная, состоит из образующих |
| Высота \( h \) | Перпендикулярное расстояние между основаниями |
| Радиусы \( R \) и \( r \) | Радиусы большего и меньшего оснований соответственно |
| Образующая \( l \) | Расстояние между краями оснований |
Математическая формула для расчета
Математическая формула для расчета объема усеченного конуса основывается на площадях его оснований и высоте. Формула объема \( V \) усеченного конуса задается следующим образом:
где:
- \( R \) и \( r \) - радиусы большего и меньшего оснований усеченного конуса соответственно,
- \( h \) - высота усеченного конуса, измеряемая как перпендикулярное расстояние между двумя основаниями.
Эта формула позволяет точно определить объем усеченного конуса, зная размеры его оснований и высоту. Важно отметить, что формула применима как для правильных, так и для неправильных усеченных конусов, поскольку она зависит только от размеров оснований и высоты.
Принцип расчета основан на том, что объем усеченного конуса равен разности объемов двух конусов – большего конуса с радиусом основания \( R \) и высотой, равной сумме \( h \) и высоты меньшего конуса, вписанного в усеченный, с радиусом \( r \).
Таким образом, понимание этой формулы и способность применять ее на практике позволяют точно рассчитывать объемы усеченных конусов в различных практических и теоретических задачах.
Практическое применение
Знания о расчете объема усеченного конуса имеют важное значение во многих областях, от инженерии и архитектуры до образования и науки. Вот некоторые из наиболее значимых примеров практического использования этих знаний:
Инженерия и проектирование. Усеченные конусы часто встречаются в проектировании различных инженерных сооружений и механизмов. Расчет их объема помогает в определении веса и материалов, необходимых для их создания. Примерами могут служить элементы мостовых конструкций или частей машин.
Архитектура. В архитектуре усеченный конус используется для создания уникальных форм зданий и сооружений. Знание его объема помогает архитекторам в планировании пространства и определении структурной нагрузки.
Образование и наука. В образовательных учреждениях понимание того, как рассчитать объем усеченного конуса, является важной частью курсов геометрии и математики. В научных исследованиях эти знания применяются для изучения физических свойств различных материалов и элементов.
Промышленное производство. В промышленности расчет объема усеченного конуса необходим при проектировании различных контейнеров, труб, вентиляционных систем и других продуктов.
Космическая отрасль. В аэрокосмической индустрии усеченные конусы используются в конструкциях ракет и космических аппаратов. Точные расчеты их объемов критически важны для обеспечения правильного баланса топлива и обеспечения стабильности полета.
Таким образом, знание того, как рассчитывается объем усеченного конуса, открывает широкие возможности для его практического применения в различных отраслях, влияя на развитие технологий и научные исследования.
Заключение
Усеченный конус – это не просто абстрактная геометрическая фигура, но и объект, имеющий широкое применение в реальном мире. От архитектуры до аэродинамики, от кулинарии до промышленного дизайна – понимание и умение правильно рассчитать объем усеченного конуса имеет огромное практическое значение. Знание этих принципов позволяет более глубоко понять и оценить множество объектов и явлений вокруг нас.
В этой статье мы рассмотрели ключевые аспекты усеченного конуса – от его геометрического описания до математических формул для расчета объема. Эти знания не только расширяют наше понимание геометрии как науки, но и предоставляют практические инструменты для решения реальных задач в самых разных сферах деятельности.
Комментарии к калькулятору
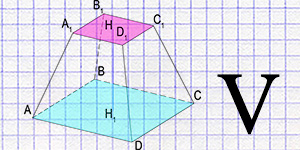
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету
Калькулятор для расчета объема конуса через высоту или апофему и площадь основания или радиус основания.
Перейти к расчету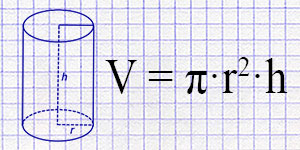
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету