Калькулятор объема цилиндра

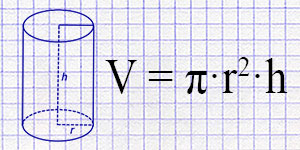
Калькулятор позволяет рассчитать объем цилиндра через его высоту и один из параметров: радиус, диаметр или площадь основания. Формула для расчета объема: V = π · r² · h или S = π · d²/4 · h. В практических задачах формула вычисления объема цилиндра применяется при расчете объема и массы различных прутков, цилиндрических заготовок и т.п.

Исходные данные

Радиус цилиндра

Высота конуса

Цилиндр - одна из фундаментальных геометрических фигур, которая играет значительную роль как в теоретической математике, так и в многочисленных практических приложениях. Это простая, но универсальная форма, обнаруживаемая в природе, архитектуре, машиностроении и многих других областях. Отличительной чертой цилиндра является его прямая или кривая боковая поверхность, образованная параллельными линиями, соединяющими два идентичных круга или эллипсы.

Объем цилиндра - ключевая характеристика, важная для решения широкого спектра задач: от простых вычислений в школьной программе до сложных инженерных расчетов в строительстве и проектировании. Понимание того, как вычислить объем цилиндра, может помочь в разнообразных ситуациях - от определения вместимости контейнера до расчета материалов, необходимых для конструкции.

Геометрическое Описание Цилиндра

Цилиндр представляет собой трехмерную геометрическую фигуру, характеризующуюся двумя параллельными и равными основаниями, соединенными боковой поверхностью. Вот ключевые характеристики цилиндра:

Основания

Форма: Круглая (в случае прямого кругового цилиндра) или эллиптическая (для эллиптического цилиндра).
Расположение: Параллельно друг другу на равном расстоянии.

Боковая Поверхность

Форма: Прямоугольник, обернутый вокруг оси цилиндра. В прямом цилиндре боковая поверхность перпендикулярна основаниям.

Высота (h)

Описание: Перпендикулярное расстояние между двумя основаниями.
Важность: Определяет длину боковой поверхности.

Радиус (r) и Диаметр (d)

Радиус: Расстояние от центра основания до его края.
Диаметр: Двойной радиус, наибольшее расстояние через центральную точку основания.

Ось Цилиндра

Описание: Воображаемая линия, соединяющая центры оснований.
Роль: Определяет направление и ориентацию цилиндра.

Типы Цилиндров

Прямой Цилиндр: Основания перпендикулярны оси.
Наклонный Цилиндр: Основания наклонены относительно оси.

Таблица Характеристик Цилиндра

Характеристика	Описание
Основания	Два параллельных круга разного радиуса
Боковая поверхность	Наклонная, состоит из образующих
Высота (h)	Перпендикулярное расстояние между основаниями
Радиусы (R и r)	Радиусы большего и меньшего оснований соответственно
Образующая (l)	Расстояние между краями оснований

Математические Основы

Цилиндр, как и любая другая геометрическая фигура, имеет свои уникальные формулы для расчета объема. Важно понимать, как эти формулы выводятся и применяются для вычисления объема цилиндра.

Формула Объема Цилиндра

Объем (V) цилиндра вычисляется по формуле:

\[ V = \pi r^2 h \]

где:

r - радиус основания цилиндра,
h - высота цилиндра,
\(\pi\) - математическая константа, приблизительно равная 3.14159.

Принципы Расчета

Радиус: Чтобы найти объем, необходимо знать радиус основания. Радиус - это расстояние от центра круглого основания до его края.
Высота: Высота цилиндра измеряется как перпендикулярное расстояние между двумя основаниями.
Использование \(\pi\): Константа \(\pi\) используется для вычисления площади круга, которая затем умножается на высоту для получения объема.

Примеры Расчета

1. Цилиндр с радиусом 3 м и высотой 5 м:

\[ V = \pi \times 3^2 \times 5 = 9\pi \times 5 \approx 141.37 \text{ м}^3 \]

2. Цилиндр с радиусом 2 м и высотой 10 м:

\[ V = \pi \times 2^2 \times 10 = 4\pi \times 10 \approx 125.66 \text{ м}^3 \]

Эти примеры иллюстрируют базовый принцип расчета объема цилиндра и демонстрируют, как изменение радиуса и высоты влияет на объем. Важно понимать эти математические принципы для корректного вычисления объемов в различных практических задачах.

Практическое применение расчета

Инженерия и строительство: цилиндры широко используются в конструкциях зданий, водонапорных башнях, хранилищах газа и жидкостей. Знание их объема помогает в расчете материалов и планировании использования пространства.
В различных промышленных сферах, таких как нефтегазовая, химическая, и пищевая промышленность, цилиндры используются в качестве резервуаров и танков. Расчет их объема необходим для определения вместимости.
В медицинском оборудовании, например, в кислородных баллонах и цилиндрических контейнерах для хранения, расчет объема помогает в определении емкости и дозировании.
В учебных заведениях знания о расчете объема цилиндра используются для обучения студентов основам геометрии и математики.
Повседневная жизнь: hасчет объема цилиндрических объектов, таких как бутылок, банок и бочек, помогает в определении их вместимости.

Заключение

Цилиндр, как геометрическая фигура, играет важную роль в различных областях нашей жизни. Понимание того, как рассчитать его объем, является ключевым навыком во многих профессиональных и академических областях. Этот расчет не только улучшает наше понимание геометрии, но и обеспечивает практическую пользу в инженерии, строительстве, промышленности и многих других сферах. Таким образом, знание и умение применять математические формулы для расчета объема цилиндра открывает двери для решения сложных практических задач и способствует развитию технологических и научных инноваций.

Скопировать калькулятор «Объем цилиндра»: