Объем конуса
Конус - это одна из фундаментальных геометрических фигур, которая нашла широкое применение в различных областях науки, техники и искусства. Он представляет собой тело вращения, образованное вращением правильного треугольника вокруг одной из своих сторон. Конус характеризуется круглым основанием и вершиной, которая находится над центром основания.
Исторически конусы использовались в архитектуре, инженерии и даже в религиозных символах. От древних времен до современных дней они служили как практическим, так и эстетическим целям. В архитектуре древнего Египта и Греции конические формы можно встретить в дизайне зданий и монументов. В современном мире конус находит свое применение в аэродинамике, где его форма используется для создания объектов с минимальным сопротивлением воздуха, таких как носы ракет и самолетов.
Геометрическое описание конуса
Конус - это геометрическое тело, которое состоит из круглого основания и наклонной поверхности, сходящейся в одной точке, называемой вершиной. Эти основные элементы определяют форму и свойства конуса.
- Основание: круглой формы, расположено горизонтально.
- Боковая поверхность: наклонная, образующая круговой сектор.
- Вершина: точка, расположенная над центром основания, где сходятся все линии боковой поверхности.
Таблица характеристик конуса:
| Характеристика | Описание |
|---|---|
| Основание | Круг |
| Вершина | Центральная точка над основанием |
| Высота (h) | От вершины до основания |
| Радиус (r) | Расстояние от центра основания до его края |
| Образующая (l) | От вершины до края основания |
Формулы для конуса:
- Высота (h): перпендикулярное расстояние от вершины до основания.
- Радиус (r): расстояние от центра основания до его края.
- Образующая (l): расстояние от вершины до края основания, рассчитывается по теореме Пифагора как \( l = \sqrt{h^2 + r^2} \).
Математическая формула для расчета объема конуса
Объем конуса рассчитывается на основе его геометрических характеристик – высоты и радиуса основания. Формула для вычисления объема конуса \( V \) выражается следующим образом:
V = \(\frac{1}{3} \pi r^2 h\)
где:
- \( r \) – радиус основания конуса,
- \( h \) – высота конуса, измеряемая от вершины до центра основания.
Эта формула основана на предположении, что основание конуса является кругом, а высота проведена перпендикулярно основанию. Важно отметить, что объем конуса составляет одну треть от объема цилиндра с теми же основанием и высотой.
Применение формулы
Для расчета объема конуса необходимо знать его радиус основания и высоту. Если известна образующая конуса, высоту можно вычислить, используя теорему Пифагора:
h = \(\sqrt{l^2 - r^2}\)
где \( l \) – образующая конуса. После определения всех необходимых величин можно подставить их в формулу для расчета объема.
Практическое применение знаний о объеме конуса
Знание о том, как рассчитать объем конуса, имеет множество практических применений в различных областях. От промышленного дизайна до архитектуры, от геометрии до прикладной математики, понимание объема конуса играет ключевую роль в многих сферах. Ниже приведены некоторые из основных примеров использования этих знаний:
- Архитектура и строительство: Конусообразные структуры часто используются в архитектуре, например, в куполах и башнях. Расчет их объема помогает в планировании материалов и определении структурной стабильности.
- Промышленное проектирование: В машиностроении и дизайне конусы могут применяться в составных частях машин и механизмов. Точный расчет объема необходим для определения вместимости или веса компонентов.
- Образование: В учебных заведениях знания о расчете объема конуса используются для обучения студентов основам геометрии и математики.
- Наука и исследования: В области научных исследований расчет объема конуса может применяться в физике и инженерии, например, при изучении аэродинамических или гидродинамических свойств объектов.
- Кулинария: В кулинарии форма конуса встречается в различных видах упаковки, например, в стаканчиках для мороженого. Расчет их объема помогает определить необходимое количество ингредиентов.
Таким образом, понимание того, как рассчитывается объем конуса, открывает множество возможностей для его практического применения в повседневной жизни и профессиональной деятельности.
Заключение
Объем конуса - важный геометрический элемент, играющий ключевую роль во многих областях, начиная от архитектуры и заканчивая прикладной математикой. Понимание того, как рассчитывается объем конуса, способствует развитию математического мышления и находит широкое применение в реальных задачах. От точности этих расчетов часто зависит успех многих инженерных и конструкторских проектов. Таким образом, глубокое понимание принципов расчета объема конуса является неотъемлемой частью образования и профессиональной деятельности во многих сферах.
Список литературы и ресурсы
- Жижченко А.Б., "Основы геометрии", Москва: Высшая школа, 2003.
- Иванов А.В., "Стереометрия: геометрия в пространстве", Санкт-Петербург: Издательство "Лань", 2010.
- Киселев А.П., "Элементарная математика. Геометрия", Москва: Просвещение, 1987.
- MathWorld - Wolfram Web Resource, "Cone", доступно на [http://mathworld.wolfram.com/Cone.html]
- Khan Academy, "Geometry and Volume", доступно на [https://www.khanacademy.org/math/geometry]
Эти источники предоставляют дополнительную информацию о конусах и их объемах, а также о геометрии в целом, и могут быть полезны для дальнейшего изучения темы.
Комментарии к калькулятору
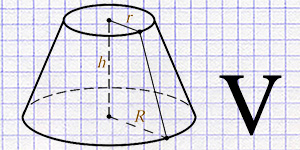
Расчет объема усеченного конуса через радиус/диаметр нижнего и верхнего основания и высоту.
Перейти к расчету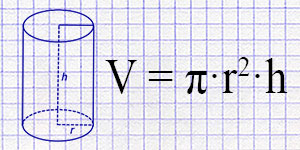
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету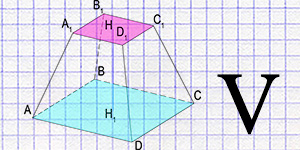
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету