Объем пирамиды

Пирамида – это уникальная геометрическая фигура, которая играет важную роль как в математике, так и в истории человечества. Эта фигура состоит из основания, которое может быть любым многоугольником, и треугольных граней, сходящихся в одной точке, называемой вершиной.
В истории пирамиды занимают особое место, особенно в архитектуре древних цивилизаций. Самыми известными примерами являются египетские пирамиды, построенные как величественные мавзолеи для фараонов. Они являются символом инженерного искусства и математических знаний древних людей.
В математике пирамида изучается в рамках стереометрии – раздела геометрии, занимающегося изучением объемных тел в пространстве. Пирамиды используются для изучения таких концепций, как объем, площадь поверхности и теоремы о треугольниках, что делает их важным элементом в образовательных программах по геометрии.
Основные типы пирамид и их свойства
Пирамиды классифицируются по типу их основания и местоположению вершины. Вот основные типы:
- Правильная пирамида: Основание является правильным многоугольником, а вершина находится прямо над центром основания. Боковые грани – равные равнобедренные треугольники.
- Неправильная пирамида: Основание может быть любым многоугольником, а вершина не обязательно находится над центром основания.
- Треугольная пирамида (тетраэдр): Все грани – треугольники. Может быть правильной (все грани – равносторонние треугольники) или неправильной.
Таблица свойств пирамид:
| Тип пирамиды | Основание | Вершина | Грани |
|---|---|---|---|
| Правильная | Правильный многоугольник | Над центром основания | Равнобедренные треугольники |
| Неправильная | Любой многоугольник | Не обязательно над центром | Различные треугольники |
| Треугольная (тетраэдр) | Треугольник | Над центром треугольника | Треугольники |
Формулы для расчета объема:
Объем пирамиды \( V \) рассчитывается по формуле: \( V = \frac{1}{3}Sh \)
Где \( S \) – площадь основания, а \( h \) – высота пирамиды, проведенная от вершины к основанию перпендикулярно ему.
Пример расчета для правильной четырехугольной пирамиды (пирамида с квадратным основанием):
Пусть сторона основания \( a = 4 \) метра, а высота \( h = 6 \) метров. Тогда:
\( S = a^2 = 4^2 = 16 \, \text{м}^2 \)
\( V = \frac{1}{3}Sh = \frac{1}{3} \times 16 \times 6 = \frac{96}{3} = 32 \, \text{м}^3 \)
Таким образом, объем данной пирамиды составляет 32 кубических метра.
Геометрические свойства пирамид
Пирамиды обладают рядом уникальных геометрических свойств, которые делают их интересными объектами для изучения. Важные аспекты включают в себя:
Стороны и Углы
- Каждая пирамида имеет базу (основание) и боковые грани.
- Основание может быть любым многоугольником, количество боковых граней равно количеству сторон основания.
- Углы между боковыми гранями и основанием называются наклонными углами.
Высота и Апофема
- Высота пирамиды (h) – перпендикулярное расстояние от вершины до основания.
- Апофема – высота боковой грани, проведенная от вершины до середины стороны основания (только для правильных пирамид).
Виды пирамид
- Правильные пирамиды имеют правильный многоугольник в основании и все боковые грани – равные равнобедренные треугольники.
- Неправильные пирамиды имеют разные боковые грани и основание может быть любым многоугольником.
Таблица характеристик различных видов пирамид
| Вид пирамиды | Основание | Высота боковой грани (Апофема) | Особенности граней |
|---|---|---|---|
| Правильная | Правильный многоугольник | Равны | Равнобедренные треугольники |
| Неправильная | Любой многоугольник | Различны | Разносторонние треугольники |
Расчет объема пирамиды
Пирамида является классическим объектом в геометрии, и расчет ее объема имеет большое значение как в теоретических, так и в прикладных аспектах геометрии и архитектуры.
Общая формула для объема
Формула для расчета объема пирамиды зависит от площади ее основания и высоты. Объем V пирамиды вычисляется по формуле:
V = 1/3 × Площадь основания × Высота
Вычисление площади основания
Площадь основания S зависит от типа многоугольника, лежащего в его основании:
- Для квадрата: S = сторона²
- Для прямоугольника: S = длина × ширина
- Для правильного треугольника: S = \( \frac{\sqrt{3}}{4} \) × сторона²
- Для многоугольной пирамиды: S = (количество сторон × длина стороны × апофема) / 2 (Апофема - это перпендикуляр, опущенный из центра основания на одну из его сторон)
Примеры расчета объема
Для квадратной пирамиды
- Пусть сторона основания равна 4 м, а высота пирамиды – 6 м.
- Площадь основания: 4² = 16 м²
- Объем: V = 1/3 × 16 × 6 = 32 м³
Для треугольной пирамиды
- Пусть сторона основания равна 3 м, а высота пирамиды – 5 м.
- Площадь основания: √3/4 × 3² ≈ 3.897 м²
- Объем: V = 1/3 × 3.897 × 5 ≈ 6.495 м³
Для многоугольной пирамиды
- Предположим, что основание пирамиды представляет собой правильный многоугольник с количеством сторон \( n \) и длиной стороны \( a \), а высота пирамиды \( h \).
- Для примера возьмем пирамиду с пятиугольным основанием, где \( n = 5 \) и \( a = 3 м \), а высота \( h = 5 м \).
- Площадь основания многоугольной пирамиды можно рассчитать по формуле: Площадь основания = \( \frac{n \times a^2}{4 \times \tan(\pi/n)} \). В данном случае, Площадь основания ≈ \( \frac{5 \times 3^2}{4 \times \tan(\pi/5)} \) ≈ 15.48 м²
- Таким образом, объем многоугольной пирамиды будет: V = \(\frac{1}{3} \times 15.48 \times 5 \) ≈ 25.80 м³
Для тетраэдра
Тетраэдр - это вид пирамиды с треугольным основанием, где все четыре грани являются равносторонними треугольниками.
- Предположим, что длина стороны тетраэдра равна \( a = 4 м \).
- Площадь основания тетраэдра (равностороннего треугольника) можно вычислить по формуле: Площадь основания = \( \frac{\sqrt{3}}{4} \times a^2 \). В данном случае, Площадь основания = \( \frac{\sqrt{3}}{4} \times 4^2 \) ≈ 6.928 м².
- Высоту тетраэдра можно вычислить по формуле: Высота = \( \sqrt{\frac{2}{3}} \times a \). В данном случае, Высота = \( \sqrt{\frac{2}{3}} \times 4 \) ≈ 3.266 м.
- Таким образом, объем тетраэдра будет: V = \( \frac{1}{3} \times 6.928 \times 3.266 \) ≈ 7.542 м³.
Заключение
Изучение объема пирамиды представляет собой важный аспект в области геометрии и применяется в самых разнообразных сферах, начиная от архитектуры и заканчивая образованием. Понимание принципов расчета объема пирамиды не только способствует развитию математического и аналитического мышления, но и имеет практическое значение в реальном мире.
Пирамида, как геометрическая фигура, служит отличным примером того, как абстрактные математические понятия находят свое воплощение в конкретных объектах и конструкциях. От древних времен до наших дней пирамиды привлекают внимание своей уникальной формой и геометрическими свойствами. Их присутствие в архитектуре, искусстве, науке и многих других областях подчеркивает универсальность и значимость этой фигуры.
Комментарии к калькулятору
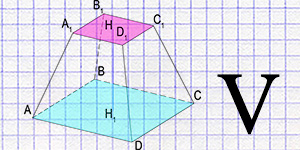
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету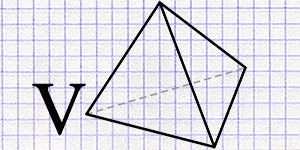
Нахождение объема тетраэдра через длины ребер, радиусы списанной и описанной окружностей.
Перейти к расчету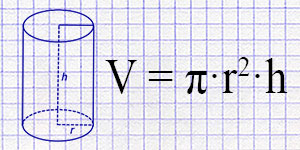
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету