Калькулятор объема тетраэдра
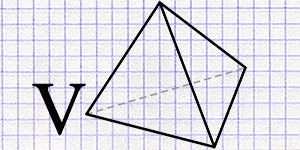
Тетраэдр, одна из самых простых и в то же время уникальных геометрических фигур, играет ключевую роль в изучении пространственной геометрии и находит широкое применение в самых разнообразных областях. Эта фигура представляет собой многогранник, состоящий из четырех треугольных граней, которые сходятся в четырех вершинах и соединяются шестью ребрами. В зависимости от формы граней, тетраэдры бывают правильными и неправильными, где в правильном тетраэдре все грани являются равносторонними треугольниками.
Исторически, тетраэдры использовались в различных культурах и цивилизациях для символизации элементов и концепций, связанных с пространством и структурой. В математике тетраэдр служит важным объектом для изучения стереометрии и топологии. Его простая, но многогранная структура позволяет углубить понимание трехмерных форм и их свойств.
Геометрическое Описание
Тетраэдр представляет собой трехмерную фигуру в пространстве, характеризующуюся четырьмя треугольными гранями, четырьмя вершинами и шестью ребрами. В зависимости от формы граней тетраэдры делятся на разные типы/
Основные элементы тетраэдра:
| Грани |
Всего: 4 грани. Форма: Каждая грань – треугольник. В правильном тетраэдре все грани – равносторонние треугольники. |
| Рёбра |
Всего: 6 рёбер. Особенности: В правильном тетраэдре все рёбра равны по длине. |
| Вершины |
Всего: 4 вершины. Особенности: В каждой вершине сходятся три грани и три ребра. |
Типы тетраэдров:
| Тип | Свойства |
|---|---|
| Правильный (Равносторонний) тетраэдр |
Все грани представляют собой равносторонние треугольники. Все рёбра равны по длине. |
| Неправильный тетраэдр |
Грани могут быть различными треугольниками. Рёбра могут быть различной длины. |
Геометрические свойства:
- В правильном тетраэдре все углы между рёбрами равны, и каждый угол между гранями равен примерно 70.53°.
- Правильный тетраэдр обладает высокой степенью симметрии.
- В тетраэдре отсутствуют диагонали в классическом понимании, как в многогранниках с более чем четырьмя гранями.
Эти характеристики определяют уникальные свойства тетраэдра и влияют на его использование в различных практических и теоретических приложениях.
Математические основы
Для расчета объема тетраэдра используются различные математические формулы, в зависимости от типа тетраэдра и известных параметров.
Объем правильного тетраэдра
Для правильного тетраэдра, где все стороны равны, объем \(V\) рассчитывается по формуле:
где \(a\) - длина ребра тетраэдра.
Через высоту и площадь основания
Если известны высота \(h\) тетраэдра и площадь основания \(A\), объем вычисляется как:
Через длины ребер
Для тетраэдра с различными длинами ребер \(a\), \(b\), \(c\), \(d\), \(e\), и \(f\), объем \(V\) можно рассчитать, используя формулу Кэли-Менгера:
где \(X = (b^2 + c^2 - e^2)\), \(Y = (a^2 + c^2 - f^2)\), \(Z = (a^2 + b^2 - d^2)\).
Через радиус вписанной окружности
Если известен радиус вписанной в тетраэдр сферы \(r_{впис}\), то объем \(V\) правильного тетраэдра можно найти по формуле:
Через радиус описанной окружности
Для тетраэдра с известным радиусом описанной около него сферы \(r_{опис}\), объем \(V\) вычисляется следующим образом:
Примеры Расчета
- Для правильного тетраэдра с ребром длиной 4 м, объем: \(V = \frac{4^3}{6 \sqrt{2}} \approx 9.24\) кубических метров.
- При высоте 5 м и площади основания 10 квадратных метров, объем: \(V = \frac{1}{3} \times 10 \times 5 = 16.67\) кубических метров.
Эти формулы позволяют точно рассчитать объем тетраэдра, что является важным аспектом во многих областях, включая архитектуру, инженерию и математику.
Практическое применение
В современном мире тетраэдры находят практическое применение в архитектуре, инженерии, дизайне и даже в искусстве. Они служат основой для создания различных конструкций, от простых декоративных объектов до сложных архитектурных элементов.
Архитектура и строительство:
- Тетраэдры используются в архитектуре для создания оригинальных и устойчивых конструкций, таких как каркасные дома или игровые площадки.
- В строительстве тетраэдрические элементы могут использоваться для укрепления конструкций и распределения нагрузок.
Дизайн и искусство:
- Тетраэдры находят применение в дизайне интерьеров и скульптурах, предоставляя уникальные геометрические формы.
- В ювелирном искусстве тетраэдрические формы используются для создания оригинальных украшений.
Образование и наука:
- Расчет объема тетраэдра является важной частью учебной программы по геометрии.
- В научных исследованиях тетраэдры используются для моделирования молекулярных структур и других комплексных систем.
Игры и развлечения:
- Тетраэдрические элементы применяются в настольных и видеоиграх, а также в головоломках.
Заключение
Тетраэдр, как одна из основных геометрических фигур, играет значительную роль в различных областях человеческой деятельности. От архитектуры и дизайна до образования и научных исследований, знание того, как рассчитать его объем, является важным навыком. Расчет объема тетраэдра помогает понять сложные геометрические принципы и находит практическое применение в решении реальных задач. Эти знания способствуют развитию технологий, улучшают проектные и аналитические навыки, а также стимулируют творческий подход в разных сферах деятельности.
Комментарии к калькулятору
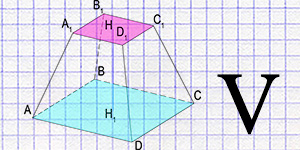
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету
Калькулятор расчета объема пирамиды через высоту и площадь основания или одну из сторон основания.
Перейти к расчету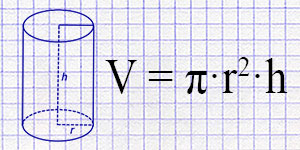
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету