Калькулятор объема шара

Шар является одной из наиболее узнаваемых и важных геометрических фигур, широко используемых во многих областях науки и техники. Эта простая, но в то же время универсальная форма привлекала внимание математиков и философов со времен древности.
Геометрически шар определяется как множество точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от центральной точки. Это расстояние называется радиусом шара. Впервые понятие шара и способы вычисления его объема были исследованы в Древней Греции, и с тех пор эта фигура занимает центральное место в изучении геометрии.
Геометрическое описание шара
Шар представляет собой идеально круглую трехмерную фигуру, каждая точка на поверхности которой равноудалена от центра. Эта фундаментальная геометрическая фигура обладает рядом характеристик и свойств:
- Центр: центральная точка шара, от которой все точки на его поверхности равноудалены.
- Радиус (r): расстояние от центра шара до любой точки на его поверхности.
- Диаметр (d): наибольшее расстояние между двумя точками на поверхности шара, проходящее через центр. Диаметр равен удвоенному радиусу (d = 2r).
- Поверхность: внешняя граница шара, каждая точка которой находится на равном расстоянии от центра.
- Объем: пространство, заключенное внутри поверхности шара.
Таблица характеристик шара:
| Характеристика | Описание |
|---|---|
| Центр | Центральная точка шара |
| Радиус (r) | От центра до поверхности шара |
| Диаметр (d) | Наибольшее расстояние через центр шара |
| Поверхность | Внешняя граница шара |
| Объем | Пространство внутри шара |
Формулы, связанные с шаром:
- Площадь поверхности шара: \( A = 4\pi r^2 \)
- Объем шара: \( V = \frac{4}{3}\pi r^3 \)
Математическая формула
Математическая формула для расчета объема шара основана на его радиусе. Объем шара - это количество пространства, занимаемого шаром, и его можно вычислить, используя радиус шара.
Объем V шара радиусом r определяется формулой:
где \(\pi\) - математическая константа, приблизительно равная 3.14159.
Как использовать формулу: Чтобы найти объем шара, нужно возвести радиус шара в куб (умножить радиус на себя три раза) и умножить результат на \(\frac{4}{3} \pi\).
Пример расчета объема: если радиус шара равен 5 метрам, то объем шара будет рассчитываться как:
Эта формула является ключевым инструментом в геометрии и прикладных науках, позволяя рассчитывать объемы сферических объектов в различных областях, от архитектуры до астрономии.
Объем шара, вписанного в куб
Если шар вписан в куб, то диаметр шара равен длине ребра куба. Пусть длина ребра куба равна a, тогда радиус шара r = \frac{a}{2} и объем шара:
Объем шара, вписанного в тетраэдр
Для шара, вписанного в правильный тетраэдр, радиус шара можно найти через длину ребра тетраэдра a. Радиус шара r составляет примерно одну треть от высоты тетраэдра. Формула радиуса вписанного шара: r = \frac{a \sqrt{6}}{12}, и объем шара:
Практическое применение знаний о объеме шара
Знание о том, как рассчитать объем шара, имеет широкий спектр практических применений в различных областях, включая науку, инженерию и повседневную жизнь. Некоторые из основных примеров:
- Наука и инженерия: в этих областях знания о объеме шара используются для расчета вместимости сферических емкостей, проектирования оптических приборов и изучения астрономических объектов.
- В дизайне и архитектуре сферические формы применяются для создания уникальных конструкций, например, в купольных зданиях и декоративных элементах.
- В медицине знание объема шара используется при проектировании медицинского оборудования, такого как имплантаты и протезы.
- Понимание объема шара является ключевым элементом в обучении геометрии и математики, помогая студентам развивать пространственное мышление и аналитические навыки.
Заключение
Шар как геометрическая фигура играет важную роль во многих областях человеческой деятельности. Понимание того, как вычисляется его объем, является фундаментальным навыком в геометрии и имеет множество практических применений. От архитектуры до астрономии, от медицины до образования - знания о объеме шара оказывают влияние на различные аспекты нашей жизни и работы.
Комментарии к калькулятору
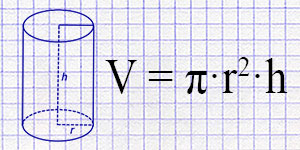
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету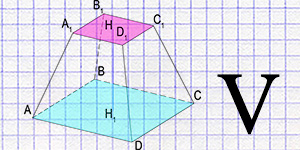
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету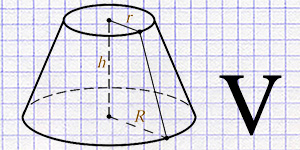
Расчет объема усеченного конуса через радиус/диаметр нижнего и верхнего основания и высоту.
Перейти к расчету