Калькулятор объема призмы

Призма – это многогранник, образованный двумя равными и параллельными многоугольниками, которые называются основаниями призмы, и прямоугольниками или параллелограммами, соединяющими соответствующие стороны оснований, называемыми боковыми гранями. Призмы классифицируются по количеству углов в основании и по расположению боковых граней относительно оснований: прямая призма имеет боковые грани, перпендикулярные основаниям, а наклонная – нет.
Существуют различные виды призм: правильные, у которых основания – правильные многоугольники и боковые ребра равны, и неправильные, где условия правильности не выполняются. Ключевым параметром призмы, наряду с площадью поверхности, является её объем – количество пространства, ограниченного её поверхностями.
Геометрическое описание призмы
Призма является трехмерной фигурой в геометрии, которая обладает интересными и важными свойствами, делая её применимой в различных областях науки и техники. Для полного понимания призмы, важно рассмотреть её геометрические характеристики подробнее.
Основные элементы призмы:
- Основания призмы: Два параллельных и равных многоугольника, расположенных в разных плоскостях. Основания определяют форму призмы и могут быть любыми многоугольниками, от треугольников до многоугольников с большим числом сторон.
- Боковые грани: Прямоугольники или параллелограммы, соединяющие соответствующие стороны двух оснований. Количество боковых граней равно количеству сторон многоугольника основания.
- Рёбра: Отрезки, соединяющие соответствующие вершины оснований и являющиеся сторонами боковых граней. Рёбра призмы делятся на боковые рёбра и рёбра оснований.
- Вершины: Точки, в которых сходятся рёбра призмы. Количество вершин в призме в два раза больше количества вершин основания.
Типы призм:
- Прямая призма: Боковые рёбра перпендикулярны основаниям, а боковые грани — прямоугольники.
- Наклонная призма: Боковые рёбра наклонены к основаниям, а боковые грани — параллелограммы.
Особенности призмы:
- Прямая призма с правильным многоугольником в основании называется правильной призмой.
- Объем призмы определяется как произведение площади основания на высоту призмы (расстояние между основаниями).
Понимание этих геометрических особенностей призмы является ключевым для изучения её свойств и применения в решении задач.
Математическая формула для расчета объема призмы
Основной математический принцип, лежащий в основе расчета объема призмы, заключается в умножении площади основания призмы на её высоту. Эта формула универсальна и применима к любому типу призмы, независимо от формы её основания.
Формула объема призмы:
\[ V = S \cdot h \]
где:
- \(V\) — объем призмы,
- \(S\) — площадь основания призмы,
- \(h\) — высота призмы, т.е., перпендикулярное расстояние между основаниями.
Применение формулы:
- Для прямой призмы с треугольным основанием, где площадь основания (\(S\)) может быть найдена как \(\frac{1}{2} \cdot основание \cdot высота\) треугольника, и высота призмы (\(h\)) равна расстоянию между основаниями.
- В случае прямой призмы с прямоугольным основанием, \(S\) рассчитывается как произведение длины на ширину основания.
- Для наклонной призмы, формула остается той же, но важно правильно определить высоту, которая все еще измеряется как перпендикулярное расстояние между плоскостями оснований.
Примеры расчета:
- Если основание прямой призмы является квадратом со стороной 4 м, а высота призмы составляет 10 м, то объем рассчитывается как \( V = 4^2 \cdot 10 = 160 \) кубических метров.
- Для прямой призмы с треугольным основанием, где основание треугольника 3 м, высота треугольника 4 м, и высота призмы 6 м, объем будет \( V = \frac{1}{2} \cdot 3 \cdot 4 \cdot 6 = 36 \) кубических метров.
Эта формула позволяет быстро и точно определить объем призмы, что необходимо в многих задачах геометрии, физики и инженерии.
Методы нахождения объема призмы
Методы нахождения объема призмы зависят от типа призмы и доступных исходных данных. Основная формула объема \(V = S \cdot h\), где \(S\) — площадь основания, а \(h\) — высота призмы, может быть адаптирована для разных ситуаций:
- Прямая призма с полигоном в основании: Для прямой призмы с полигоном в основании объем находят, вычисляя площадь основания \(S\) как сумму площадей треугольников или других фигур, на которые можно разбить полигон, и умножая её на высоту \(h\).
\[V = S \cdot h\]
- Наклонная призма: Для наклонной призмы объем находят так же, как и для прямой, поскольку высота \(h\) измеряется перпендикулярно основаниям, а площадь основания \(S\) остается той же.
- Использование интегрального исчисления: В случаях, когда призма имеет переменную площадь основания вдоль высоты, объем может быть найден с помощью интегрального исчисления, интегрируя площадь поперечного сечения по высоте призмы.
\[V = \int_{a}^{b} A(x) dx\]где \(A(x)\) — площадь поперечного сечения на высоте \(x\).
- Через диагонали и углы между ними в основании: Если основание призмы — многоугольник, и известны диагонали и углы между ними, можно сначала найти площадь основания, используя теорему косинусов, а затем умножить на высоту.
- Правильная треугольная призма: Объем находят по формуле \(V = \frac{\sqrt{3}}{4} a^2 h\), где \(a\) — длина ребра основания, а \(h\) — высота призмы.
- Правильная четырехугольная призма (кубоид): Объем находят по формуле \(V = a^2 h\), где \(a\) — длина ребра основания.
- Правильная пятиугольная призма: Объем находят по формуле \(V = \frac{5}{4} a^2 h \tan(\frac{\pi}{5})\), где \(a\) — длина ребра основания.
- Правильная шестиугольная призма: Объем находят по формуле \(V = \frac{3\sqrt{3}}{2} a^2 h\), где \(a\) — длина ребра основания.
Эти методы позволяют адаптировать расчет объема призмы в зависимости от её типа и доступных измерений, обеспечивая точность и универсальность в решении геометрических задач.
Практическое применение
Архитектура и Строительство: знание объема призмы важно при проектировании и строительстве различных архитектурных структур, таких как здания, мосты и тоннели. Оно позволяет инженерам определять необходимое количество строительных и отделочных материалов, а также оценивать общую стоимость проекта.
Производство: в промышленности знания о расчете объема призмы применяются для определения объема контейнеров, баков и других хранилищ. Это позволяет оптимизировать процесс производства, управление запасами и логистику.
Образование: в образовательном процессе изучение методов расчета объема призмы способствует развитию пространственного мышления у учащихся, улучшает их аналитические навыки и понимание геометрических принципов.
Наука: в научных исследованиях, особенно в физике и химии, расчет объема призмы необходим для экспериментальной работы, например, при изучении свойств газов или жидкостей в замкнутых контейнерах.
Медицина: в медицинской индустрии, в частности в фармакологии, знание объема используется при проектировании упаковки для лекарств, а также при создании моделей для имплантации.
Заключение
Знания о расчете объема призмы имеют важное практическое значение во многих сферах человеческой деятельности. От образования и науки до инженерии, строительства и медицины — понимание, как находить объем призмы, способствует решению широкого круга задач. Этот навык помогает не только в выполнении конкретных профессиональных задач, но и в развитии аналитического мышления и пространственного восприятия, что делает его незаменимым в современном образовательном и профессиональном контексте.
Комментарии к калькулятору
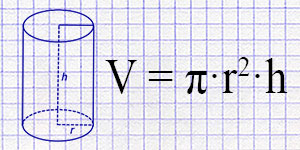
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету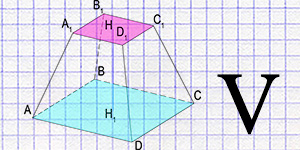
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету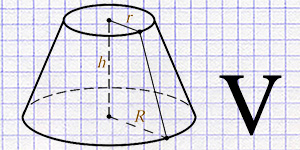
Расчет объема усеченного конуса через радиус/диаметр нижнего и верхнего основания и высоту.
Перейти к расчету