Калькулятор объема параллелепипеда
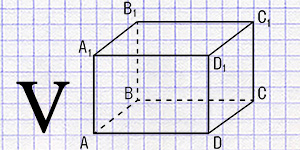
Параллелепипед – это уникальная трехмерная геометрическая фигура, имеющая широкий спектр применений в самых разных областях – от архитектуры и инженерии до математики и дизайна. Эта фигура представляет собой многогранник, образованный шестью параллелограммами, при этом каждый параллелограмм расположен противоположно и параллельно другому.
Исторически параллелепипед использовался в математике как важный инструмент для изучения пространственных свойств и отношений. Он служит базовой моделью для многих физических объектов в нашем окружающем мире, например, для коробок, зданий и других конструкций.
Геометрическое Описание
Параллелепипед является одним из ключевых объектов в геометрии, обладающим уникальными свойствами и характеристиками, которые определяют его структуру и форму.
Основные элементы:
- Грани: шесть параллелограммов, каждый из которых расположен противоположно и параллельно другому.
- Рёбра: двенадцать отрезков, соединяющих вершины параллелограммов.
- Вершины: восемь точек, в каждой из которых сходятся три ребра и три грани.
Типы параллелепипедов:
- Прямоугольный параллелепипед: все грани представляют собой прямоугольники. Частный случай прямоугольного параллелепипеда - куб.
- Наклонный параллелепипед: грани могут быть наклонены относительно основания, образуя различные типы параллелограммов.
Геометрические свойства:
- Углы: в прямоугольном параллелепипеде все углы между смежными гранями прямые (90 градусов).
- Симметрия: параллелепипед обладает элементами симметрии, особенно это заметно в случае прямоугольного параллелепипеда.
Измерения:
- Длины рёбер: в зависимости от типа параллелепипеда рёбра могут быть равны или различаться по длине.
- Диагонали: расстояния между противоположными вершинами параллелепипеда, которые могут быть использованы для расчёта его объёма при известных углах между ними.
Эти характеристики определяют внешний вид и свойства параллелепипеда, влияя на его применение в различных областях.
Математические основы
Математический расчет объема параллелепипеда основан на его геометрических характеристиках. Этот процесс включает использование определенных формул, которые позволяют точно вычислить объем фигуры.
Основная формула объема
Объем V параллелепипеда определяется произведением его длины l, ширины w и высоты h:
Расчет через диагонали и углы
Если известны диагонали и углы между ними, объем можно вычислить, используя теорему косинусов и следующую формулу:
где \(d_1\), \(d_2\), и \(d_3\) - длины трех взаимно перпендикулярных диагоналей, а \(\alpha\), \(\beta\), и \(\gamma\) - углы между этими диагоналями.
Примеры расчета
- Для прямоугольного параллелепипеда с длиной 5 м, шириной 3 м и высотой 2 м, объем: V = 5 × 3 × 2 = 30 м3.
- Через диагонали и углы: Предположим, что длины диагоналей равны 7 м, 8 м, и 9 м, а углы между ними равны 60°, 45°, и 60° соответственно. Тогда объем вычисляется по указанной выше формуле и равен примерно 149.84 кубических метров.
Понимание этих математических принципов позволяет точно вычислять объемы параллелепипедов в различных практических и теоретических задачах.
Практическое применение
- Строительство и архитектура:
- Пример: расчет объема кирпичей для строительства. Для кирпича размерами 20 см × 10 см × 5 см, объем: V = 0.20 м × 0.10 м × 0.05 м = 0.001 м3.
- Применение: определение количества материалов, планирование пространства.
- Логистика и транспортировка:
- Пример: определение объема грузовых контейнеров. Для контейнера размерами 12 м × 2.5 м × 2.5 м, объем: V = 12 м × 2.5 м × 2.5 м = 75 м3.
- Применение: планирование загрузки, оптимизация пространства, расчет стоимости перевозки.
- Производство и промышленность:
- Пример: расчет объема хранилищ. Для бункера размерами 3 м × 3 м × 4 м, объем: V = 3 м × 3 м × 4 м = 36 м3.
- Применение: определение емкости, планирование мощностей.
- Образование:
- Пример: обучение студентов геометрии и пространственному мышлению.
- Применение: развитие аналитических и пространственных навыков.
Заключение
Объем параллелепипеда - ключевой концепт в геометрии, играющий важную роль в различных областях. От строительства до образования, понимание методов расчета объема параллелепипеда и их применение на практике необходимы для успешной работы в технических и научных областях. Эти знания способствуют развитию технических и аналитических навыков, важных для решения сложных практических задач и способствуют технологическим и научным инновациям.
Комментарии к калькулятору
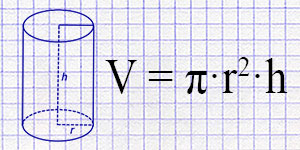
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету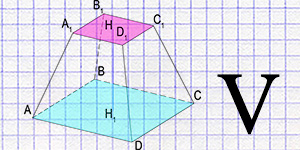
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету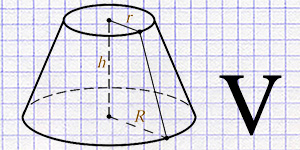
Расчет объема усеченного конуса через радиус/диаметр нижнего и верхнего основания и высоту.
Перейти к расчету