Калькулятор объема эллипсоида

Эллипсоид - это трехмерная геометрическая фигура, которая может быть представлена как трехмерное расширение эллипса. Он обладает интересными свойствами и играет важную роль в различных научных и инженерных областях, включая астрономию, физику, геодезию и даже медицинскую визуализацию.
В математике эллипсоид определяется как поверхность, образуемая точками в трехмерном пространстве, сумма расстояний которых от трех фиксированных точек (фокусов) постоянна. Эллипсоид имеет три оси симметрии, которые называются полуосями: большая ось (a), средняя ось (b) и малая ось (c). Они пересекаются в центре эллипсоида и являются перпендикулярными друг другу.
Геометрическое описание эллипсоида
Эллипсоид — это замкнутая квадратичная поверхность, которая в трехмерном пространстве представляет собой обобщение формы эллипса. Он определяется тремя ортогональными (взаимно перпендикулярными) осями: большой, средней и малой полуосями. Различают несколько типов эллипсоидов, в зависимости от соотношений между этими осями, самыми распространенными из которых являются пролатные (удлиненные) и облатные (сплюснутые) эллипсоиды.
Основные элементы
- Полуоси: Эллипсоид характеризуется тремя перпендикулярными полуосями: \(a\), \(b\), и \(c\), которые представляют собой расстояния от центра до его поверхности в соответствующем направлении. Длины полуосей определяют форму эллипсоида:
- \(a\) — длина большой (главной) полуоси,
- \(b\) — длина средней полуоси,
- \(c\) — длина малой полуоси.
- Центр: Точка пересечения трех полуосей служит центром эллипсоида и является точкой его геометрической симметрии.
Типы эллипсоидов
- Пролатный эллипсоид (удлиненный) — одна из полуосей (обычно \(a\)) длиннее двух других, которые могут быть равны или нет (\(a > b = c\)).
- Облатный эллипсоид (сплюснутый) — одна из полуосей (обычно \(c\)) короче двух других, которые могут быть равны или нет (\(a = b > c\)).
- Трехосный эллипсоид — все три полуоси имеют разные длины (\(a > b > c\)).
Геометрические свойства
- Эллипсоид обладает точечной симметрией относительно своего центра.
- Поверхность эллипсоида гладкая и непрерывная без рёбер или вершин.
- Внутренний объем эллипсоида зависит от длин его полуосей и может быть рассчитан через математические формулы.
Эллипсоиды широко используются в научных и инженерных расчетах, где необходимо учесть неидеальную сферическую форму объектов, например, в геодезии, астрономии и физике.
Математическая формула для расчета объема
Математическая формула для расчета объема эллипсоида использует длины его трех взаимно перпендикулярных полуосей: \(a\), \(b\), и \(c\). Эти полуоси определяют расстояния от центра эллипсоида до его поверхности вдоль осей \(x\), \(y\), и \(z\) соответственно.
Формула для расчета объема эллипсоида выглядит следующим образом:
\[ V = \frac{4}{3}\pi abc \]
где:
- \(V\) — объем эллипсоида,
- \(a\) — длина большой полуоси,
- \(b\) — длина средней полуоси,
- \(c\) — длина малой полуоси,
- \(\pi\) — математическая константа, приближенно равная 3.14159.
Эта формула демонстрирует, что объем эллипсоида пропорционален произведению длин его трех полуосей, а также включает в себя коэффициент, связанный с объемом шара, учитывая, что эллипсоид можно рассматривать как деформированный шар.
Пример расчета объема эллипсоида: предположим, что длины полуосей эллипсоида равны 4 м (для \(a\)), 3 м (для \(b\)) и 2 м (для \(c\)). Подставляя эти значения в формулу, получаем:
\[ V = \frac{4}{3}\pi \times 4 \times 3 \times 2 = 8\pi \approx 25.13 \text{ м}^3 \]
Таким образом, объем данного эллипсоида составляет приблизительно 25.13 кубических метров.
Связь с другими геометрическими фигурами
Эллипсоид тесно связан с другими ключевыми геометрическими фигурами, включая сферу, цилиндр и конус, а также с другими типами эллипсоидов, такими как сфероиды. Эти связи выражаются через геометрические и математические соотношения, позволяя глубже понять свойства эллипсоида и его взаимодействие с другими фигурами.
-
Сфера как частный случай эллипсоида: Когда все три полуоси эллипсоида равны (\(a\)=\(b\)=\(c\)), он становится сферой. Это показывает, что сфера является специфическим типом эллипсоида, где все точки на поверхности равноудалены от центра.
-
Сфероиды: Сфероиды – это эллипсоиды вращения, имеющие две равные полуоси. Пролатный (вытянутый) сфероид образуется вращением эллипса вокруг его малой оси, а облатный (сплюснутый) сфероид – вокруг большой оси. Эти формы важны для описания формы Земли и других планет.
-
Соотношение с цилиндром и конусом: В определенных условиях эллипсоид может быть вписан или описан вокруг цилиндра или конуса, создавая интересные геометрические соотношения. Например, максимальный эллипсоид, который может быть вписан в данный цилиндр, или минимальный эллипсоид, который может описать данный конус, имеют важное значение в геометрии и оптимизации.
-
Эллипсоиды в координатных системах: В декартовых, цилиндрических и сферических координатах эллипсоиды могут быть описаны уравнениями, отражающими их геометрические свойства. Эти уравнения помогают в анализе сложных пространственных структур и в визуализации трехмерных форм.
Применение в науке и технике
Эллипсоиды находят широкое применение в различных областях науки и техники, благодаря их уникальным геометрическим свойствам и способности моделировать множество физических и астрономических явлений.
-
Астрономия и геодезия: В астрономии эллипсоиды используются для моделирования формы планет и звезд, особенно для описания сплюснутости Земли и других планет солнечной системы. В геодезии эллипсоидальные модели Земли служат основой для точных измерений и картографии.
-
Инженерия и дизайн: В инженерии эллипсоиды применяются при проектировании аэродинамических форм, например, в авиастроении и автомобилестроении, где они помогают минимизировать сопротивление воздуха. В дизайне и архитектуре эллипсоиды используются для создания эстетически привлекательных и функциональных форм.
-
Физика и математика: В физике эллипсоиды встречаются при изучении гравитационных полей, а также в кристаллографии и молекулярной физике для описания формы молекул и кристаллов. В математике они служат объектом для изучения комплексных пространственных структур и трансформаций.
-
Медицина: В медицинской визуализации и радиологии эллипсоидные модели используются для анализа и визуализации внутренних органов, обеспечивая более точную диагностику и планирование лечения.
-
Компьютерное моделирование и графика: В компьютерном моделировании и 3D-графике эллипсоиды используются для создания реалистичных трехмерных объектов и сцен, предоставляя мощные инструменты для визуализации и анимации.
Заключение
Эллипсоид, как фундаментальная геометрическая фигура, играет важную роль во многих областях науки и техники. Его способность точно моделировать сложные формы и структуры делает его незаменимым инструментом в астрономии, инженерии, медицине и других дисциплинах. Понимание математических основ и геометрических свойств эллипсоида открывает новые возможности для исследований и разработок, способствуя технологическому прогрессу и научным открытиям. Эллипсоиды продолжают вдохновлять ученых и инженеров на создание инновационных решений и продуктов, демонстрируя глубокую взаимосвязь между геометрией и реальным миром.
Комментарии к калькулятору
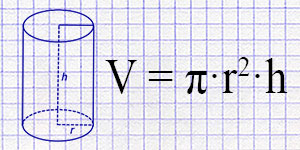
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету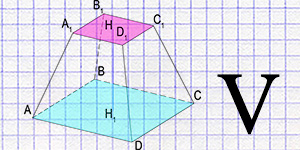
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету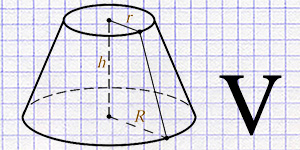
Расчет объема усеченного конуса через радиус/диаметр нижнего и верхнего основания и высоту.
Перейти к расчету