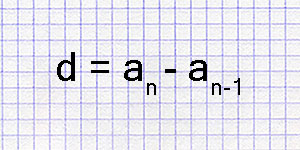Калькулятор арифметической прогрессии
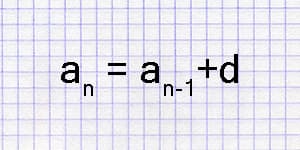
Арифметическая прогрессия - это последовательность чисел, в которой каждый член (кроме первого) получается прибавлением к предыдущему числу одной и той же постоянной разности.
Формально арифметическую прогрессию (АП) можно представить следующим образом: \(a, a+d, a+2d, a+3d, \ldots\), где \(a\) - первый член, \(d\) - разность между соседними членами.
Общий член
Общий член \(a_n\) арифметической прогрессии с первым членом \(a\) и разностью \(d\) выражается формулой: \[ a_n = a + (n-1)d \]
Сумма первых \(n\) членов
Сумма первых \(n\) членов арифметической прогрессии \(S_n\) может быть найдена по формуле: \[ S_n = \frac{n}{2} \cdot (2a + (n-1)d) \]
Свойства
- Разность: Все члены прогрессии отличаются на постоянную разность \(d\).
- Общая форма: Любой член прогрессии может быть выражен через общую формулу.
- Сумма: Формула суммы первых \(n\) членов облегчает вычисление общей суммы.
Применение
- Финансовые Расчеты: Арифметическая прогрессия используется для моделирования ежемесячных платежей, инвестиций и других финансовых операций.
- Физика: В физике арифметические прогрессии применяются при описании равномерного движения тел.
- Компьютерные Науки: Используется в алгоритмах и структурах данных.
- Статистика: При анализе временных рядов и тенденций.
Арифметическая прогрессия является важным элементом в математике и науке, предоставляя инструмент для анализа изменения величин и прогнозирования будущих значений.
Комментарии к калькулятору
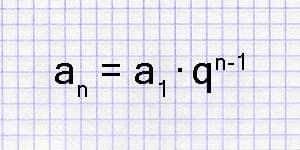
Калькулятор геометрической прогрессии позволяет найти n-й член, а также сумму ее членов.
Перейти к расчету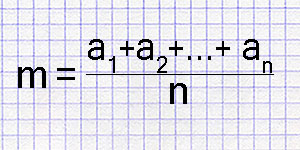
Разновидность среднего значения, определяется как сумма всех чисел, деленное на их количество.
Перейти к расчету