Среднее арифметическое нескольких чисел
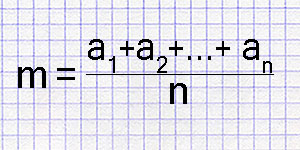
Среднее арифметическое нескольких чисел - это один из базовых статистических показателей, используемых для определения центральной тенденции набора чисел. Для его расчета суммируют все числа в наборе, а затем делят полученную сумму на количество чисел в этом наборе.
Формула среднего арифметического
Допустим, у нас есть набор чисел \( X = \{x_1, x_2, ..., x_n\} \). Среднее арифметическое этого набора обозначается как \( \bar{x} \) и рассчитывается по формуле:
\[ \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} \]
где:
- \( \sum_{i=1}^{n} x_i \) обозначает сумму всех чисел в наборе,
- \( n \) - количество чисел в наборе.
Пример расчета
Рассмотрим пример. Пусть у нас есть набор чисел 2, 3, 7, 10, и 5. Среднее арифметическое рассчитывается следующим образом:
- Суммируем все числа: \( 2 + 3 + 7 + 10 + 5 = 27 \).
- Определяем количество чисел в наборе: 5.
- Делим сумму на количество: \( \frac{27}{5} = 5.4 \).
Таким образом, среднее арифметическое данного набора чисел равно 5.4.
Значение и использование
Среднее арифметическое широко используется в статистике, экономике, образовании и многих других областях для анализа данных. Оно помогает понять общую тенденцию набора чисел и представляет собой удобный способ суммирования информации. Однако важно помнить, что среднее арифметическое может быть искажено экстремально высокими или низкими значениями в наборе, поэтому иногда его дополняют другими статистическими мерами, такими как медиана или мода.
Комментарии к калькулятору
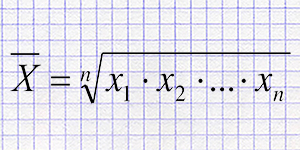
Разновидность среднего значения, которое определяется извлечением корня из произведения всех значений.
Перейти к расчету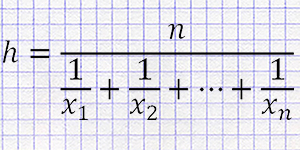
Разновидность среднего значения, определяется как обратная величина к среднему от обратных к числам.
Перейти к расчету
Подсчет среднего балла по текущим оценкам по пятибальной системе. Прогноз четвертной оценки.
Перейти к расчету