Среднее геометрическое нескольких чисел
Теги: Средние значения
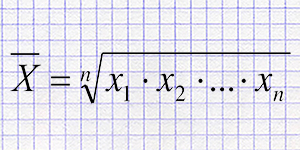
Среднее геометрическое нескольких чисел – число, равное извлеченному корню из их произведения. Пример: для ряда чисел 2, 4 и 8 среднее геометрическое g = 6. Калькулятор позволяет работать как с целыми числами, так и с дробными, например 3.5 (в этом случае разделение идет точкой, а не запятой).Среднее геометрическое определяется по формуле:
g = n√a1 · a2 · … · an,
где a1 · a2 · … · an - ряд чисел.
Комментарии к калькулятору
Количество комментариев: 0
Еще не оставлено ни одного комментария.
Похожие калькуляторы
Математика
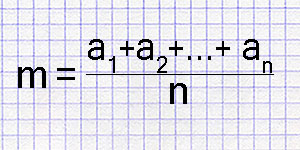
Разновидность среднего значения, определяется как сумма всех чисел, деленное на их количество.
Перейти к расчету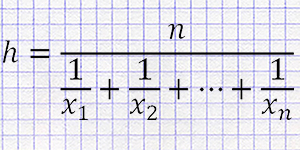
Математика
Разновидность среднего значения, определяется как обратная величина к среднему от обратных к числам.
Перейти к расчету
Математика
Подсчет среднего балла по текущим оценкам по пятибальной системе. Прогноз четвертной оценки.
Перейти к расчету