Среднее гармоническое нескольких чисел
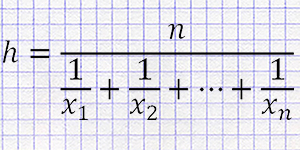
Среднее гармоническое нескольких чисел - это мера центральной тенденции, которая используется в различных областях, таких как статистика, финансы и инженерия. Этот показатель особенно полезен в ситуациях, где важны обратные значения или скорости.
Формула среднего гармонического
Среднее гармоническое для набора чисел \( X = \{x_1, x_2, ..., x_n\} \) рассчитывается по формуле:
\[ H = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}} \]
где:
- \( n \) обозначает количество чисел в наборе,
- \( \frac{1}{x_i} \) - обратное значение каждого числа в наборе.
Пример расчета
Предположим, у нас есть набор чисел 1, 4, и 9. Среднее гармоническое этих чисел рассчитывается следующим образом:
- Считаем обратные значения каждого числа: \( \frac{1}{1}, \frac{1}{4}, \frac{1}{9} \).
- Суммируем полученные значения: \( \frac{1}{1} + \frac{1}{4} + \frac{1}{9} = 1 + 0.25 + 0.1111 = 1.3611 \).
- Делим количество чисел на полученную сумму: \( \frac{3}{1.3611} \approx 2.2046 \).
Таким образом, среднее гармоническое данных чисел приблизительно равно 2.2046.
Значение и использование
Среднее гармоническое широко применяется в ситуациях, где важны скорости или обратные величины. Например, это может использоваться для вычисления средней скорости при различных скоростных ограничениях или для расчета среднего соотношения цена/качество товаров. Важной особенностью среднего гармонического является то, что оно всегда меньше или равно среднему арифметическому и геометрическому для одного и того же набора положительных чисел.
Комментарии к сервису
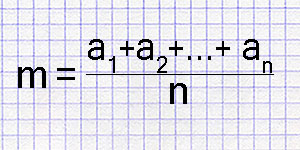
Разновидность среднего значения, определяется как сумма всех чисел, деленное на их количество.
Перейти к расчету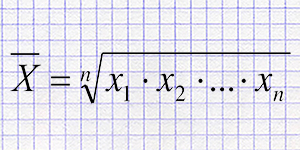
Разновидность среднего значения, которое определяется извлечением корня из произведения всех значений.
Перейти к расчету
Подсчет среднего балла по текущим оценкам по пятибальной системе. Прогноз четвертной оценки.
Перейти к расчету