Среднее квадратичное отклонение
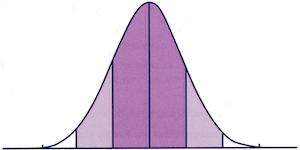
Стандартное отклонение — это статистическая мера разнообразия или изменчивости в наборе данных. Низкое стандартное отклонение указывает на то, что точки данных в целом близки к среднему значению. Высокое стандартное отклонение указывает на большую изменчивость в точках данных или большее расхождение от среднего.
Формула среднеквадратичного отклонение
Формула для вычисления выборочного стандартного отклонения:
\begin{align} s = \sqrt{\dfrac{\sum_{i=1}^{N}(X_i - \overline{X})^{2}}{N - 1}} \end{align}Формула для вычисления генерального стандартного отклонения:
\begin{align} \sigma = \sqrt{\dfrac{\sum_{i=1}^{N}(x_i - \overline{X})^{2}}{N}} \end{align}Где:
- \( s \) - выборочное стандартное отклонение,
- \( \sigma \) - генеральное стандартное отклонение,
- \( X_i \) - каждое значение в выборке,
- \( \overline{X} \) - среднее значение выборки,
- \( N \) - количество значений в выборке,
Пример вычисления
Допустим, у нас есть выборка данных о баллах, полученных студентами в некотором экзамене: 75, 80, 85, 90, 95.
Давайте вычислим выборочное и генерального стандартное отклонение для этой выборки. По формуле, оно вычисляется следующим образом:
Формула среднего значения (\( \bar{x} \)): \[ \bar{x} = \frac{75 + 80 + 85 + 90 + 95}{5} = \frac{425}{5} = 85 \]
Расчет разностей и квадратов разностей: \[ \begin{align*} 75 - 85 & : (-10)^2 = 100 \\ 80 - 85 & : (-5)^2 = 25 \\ 85 - 85 & : (0)^2 = 0 \\ 90 - 85 & : (5)^2 = 25 \\ 95 - 85 & : (10)^2 = 100 \\ \end{align*} \]
Суммирование квадратов разностей: \[ \sum{(x_i - \bar{x})^2} = 100 + 25 + 0 + 25 + 100 = 250 \]
Подставим значения в формулу для выборочного стандартного отклонения (\( s \)): \[ s = \sqrt{\frac{\sum{(x_i - \bar{x})^2}}{n-1}} = \sqrt{\frac{250}{5-1}} = \sqrt{\frac{250}{4}} = \sqrt{62.5} \approx 7.91 \]
Подставим значения в формулу для генерального стандартного отклонения (\( \sigma \)): \[ \sigma = \sqrt{\frac{\sum{(x_i - \bar{x})^2}}{n}} = \sqrt{\frac{250}{5}} = \sqrt{\frac{250}{5}} = \sqrt{50} \approx 7.07 \]
Практическое применение
Среднеквадратичное отклонение (стандартное отклонение) широко используется в статистике и анализе данных. Его практические применения включают, но не ограничиваются, следующими областями:
-
Измерение разброса данных:
Среднеквадратичное отклонение измеряет степень разброса данных относительно среднего значения. Чем больше стандартное отклонение, тем больше разброс данных.
-
Оценка Надежности Прогнозов:
В финансах и экономике среднеквадратичное отклонение используется для измерения вариации ценных бумаг и оценки риска инвестиций. Оно также применяется в оценке точности прогнозов в различных областях.
-
Контроль Качества Производства:
В производственных процессах стандартное отклонение может использоваться для контроля качества продукции. Большое отклонение может указывать на нестабильность процесса.
-
Медицинская Статистика:
В медицинской статистике среднеквадратичное отклонение может использоваться для оценки изменчивости в результатах клинических исследований или измерения разброса значений в лабораторных тестах.
-
Обучение и Тестирование:
В образовательных исследованиях среднеквадратичное отклонение может использоваться для измерения разброса оценок студентов и оценки того, насколько сильно результаты тестов отличаются друг от друга.
-
Социологические Исследования:
В социологических исследованиях среднеквадратичное отклонение может помочь измерить разброс ответов на опросы и оценить степень согласия или расхождения мнений в группе.
-
Наука о Климате:
В климатологии среднеквадратичное отклонение используется для измерения изменчивости климатических параметров, таких как температура или осадки, что важно для предсказания погоды и изучения изменений климата.
-
Инженерные Расчеты:
В инженерных расчетах стандартное отклонение может использоваться для оценки стабильности и надежности конструкций, материалов или процессов.
Комментарии к калькулятору
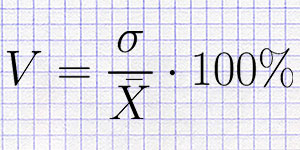
Коэффициент вариации – отношение среднеквадратичного отклонения случайной величины к ее математическому ожиданию.
Перейти к расчету
Деление столбиком или уголком поможет разделить многозначные числа за счёт разбивания деления на ряд простых шагов.
Перейти к расчету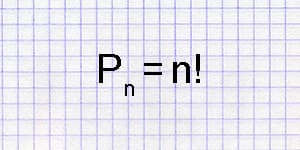
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчету