Ранг матрицы

Ранг матрицы определяется как максимальное количество линейно независимых строк или столбцов в ней. Другими словами, это наивысшее число строк (или столбцов), которые могут быть выбраны из матрицы так, чтобы они оставались линейно независимыми.
Методы вычисления ранга матрицы
- Метод Гаусса: применение элементарных преобразований строк для приведения матрицы к ступенчатому виду, и затем ранг определяется числом ненулевых строк.
- Метод миноров: ранг матрицы может быть определен с использованием миноров. Это метод, основанный на изучении детерминантов подматриц.
- Свойства ранга матрицы: ранг матрицы обладает рядом важных свойств, таких как теорема о существовании подматрицы максимального ранга и теорема о связи ранга с количеством строк и столбцов.
Пример Расчета Ранга Матрицы
Пусть у нас есть матрица:
\begin{equation*} A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix} \end{equation*}Применим элементарные преобразования и получим ступенчатый вид:
\begin{equation*} A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & -3 & -6 \\ 0 & 0 & 0 \\ \end{bmatrix} \end{equation*}Таким образом, ранг матрицы \( A \) = 2.
Свойства ранга матрицы
Ранг матрицы обладает следующими свойствами:
- Ранг нулевой матрицы равен 0.
- Ранг матрицы квадратной матрицы не превышает ее порядка.
- Ранг суммы матриц не превосходит суммы рангов матриц.
- Ранг произведения матриц не превосходит наименьшего из рангов сомножителей.
Практическое применение
- Системы линейных уравнений: ранг матрицы используется для определения совместности систем линейных уравнений и нахождения их решений.
- Анализ данных: в контексте машинного обучения и статистики, ранг матрицы применяется для уменьшения размерности данных и извлечения важных признаков.
- Управление и контроль: в инженерии и системах управления, ранг матрицы используется для анализа устойчивости и управляемости систем.
Ранг матрицы – это ключевой элемент линейной алгебры, который находит применение в различных областях науки и техники. Его понимание позволяет эффективно решать линейные системы, анализировать данные и создавать устойчивые системы управления.
Комментарии к калькулятору
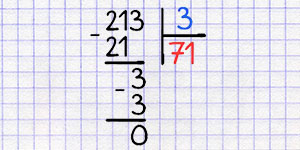
Деление столбиком или уголком поможет разделить многозначные числа за счёт разбивания деления на ряд простых шагов.
Перейти к расчету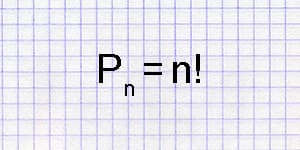
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчету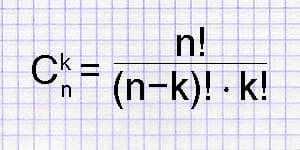
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Перейти к расчету