Пересечение множеств
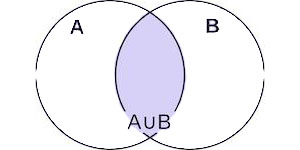
Пересечение множеств - это операция, результатом которой является множество, содержащее только те элементы, которые присутствуют в каждом из исходных множеств. Обозначается символом \( \cap \). Если A и B - два множества, то их пересечение обозначается как \( A \cap B \).
Математическая формулировка: \( A \cap B = \{ x \mid x \in A \text{ и } x \in B \} \)
Интуитивное понимание
Интуитивно пересечение множеств можно представить как область, где пересекаются множества A и B. Если A представляет собой множество красных шаров, а B - множество больших шаров, то \( A \cap B \) будет содержать только те шары, которые красные и большие одновременно.
Примеры применения
Теория множеств.Пересечение множеств играет фундаментальную роль в теории множеств и многих других математических дисциплинах. Он используется для определения свойств общих элементов множеств, что позволяет строить более сложные структуры и операции.
Логика. Пересечение множеств используется при решении логических задач. Например, если A - множество студентов, сдавших экзамен, и B - множество студентов, присутствующих на лекции, то \( A \cap B \) даст нам студентов, сдавших экзамен и присутствующих на лекции.
Анализ данных. В области анализа данных пересечение множеств может быть использовано для выделения общих элементов в двух различных наборах данных. Например, если у нас есть два списка пользователей, зарегистрировавшихся и совершивших покупки, \( A \cap B \) даст нам пользователей, зарегистрировавшихся и совершивших покупки.
Свойства пересечения множеств
- Коммутативность: \( A \cap B = B \cap A \)
- Ассоциативность: \( A \cap (B \cap C) = (A \cap B) \cap C \)
- Идемпотентность: \( A \cap A = A \)
Комментарии к калькулятору
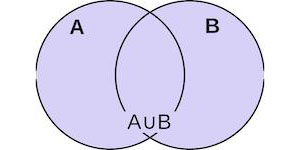
Объединение множеств А и В называется множество А ∪ В, содержащее в себе все элементы исходных множеств.
Перейти к расчету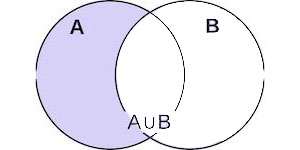
Разностью множества А и В, называется множество, содержащее элементы из множества А, но не входящие в В.
Перейти к расчету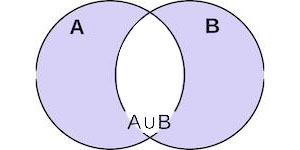
Симметрическая разность - множество, содержащее непересекающиеся элементы.
Перейти к расчету