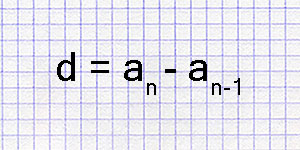Разность множеств
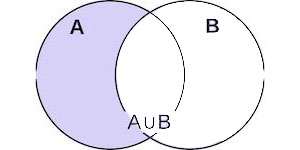
Разность множеств - это операция, результатом которой является множество, содержащее все элементы первого множества, которые не принадлежат второму множеству. Обозначается символом "∖" или "-". Если у нас есть множества A и B, то разность A и B обозначается как \(A - B\) или \(A \setminus B\).
Математическая формулировка: \(A - B = \{ x \mid x \in A \text{ и } x \notin B \}\)
Интуитивное понимание
Интуитивно разность множеств можно представить как выделение тех элементов из первого множества, которые не имеют совпадений во втором множестве. Например, если A - множество всех студентов в классе, а B - множество студентов, участвующих в спортивных мероприятиях, то разность A и B даст множество студентов, не участвующих в спортивных мероприятиях.
Примеры применения
Теория множеств: разность множеств используется для выделения уникальных элементов, принадлежащих одному множеству, но не принадлежащих другому.
Логика: в логике разность множеств может быть использована для анализа условий "не".
Анализ данных: В области анализа данных разность множеств может применяться для выявления уникальных значений или исключения определенных элементов из наборов данных.
Свойства разности множеств
- Некоммутативность: обычно \(A - B \neq B - A\).
- Антисимметричность: если \(A - B = \varnothing\), то и \(B - A = \varnothing\).
- Идемпотентность: \(A - A = \varnothing\).
Комментарии к калькулятору
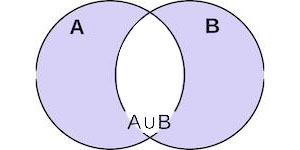
Симметрическая разность - множество, содержащее непересекающиеся элементы.
Перейти к расчету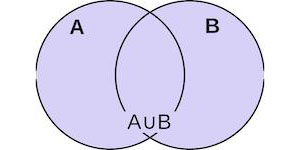
Объединение множеств А и В называется множество А ∪ В, содержащее в себе все элементы исходных множеств.
Перейти к расчету