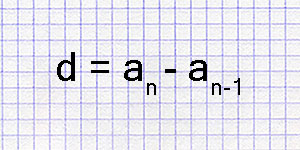Симметрическая разность множеств
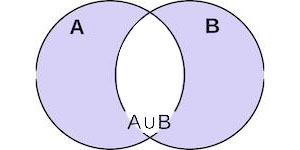
Симметрическая разность множеств - это операция, результатом которой является множество, содержащее все элементы, принадлежащие только одному из исходных множеств. Обозначается символом "△" или "\(\oplus\)". Если у нас есть множества A и B, то симметрическая разность A и B обозначается как \(A \triangle B\) или \(A \oplus B\).
Математическая формулировка: \(A \triangle B = (A \setminus B) \cup (B \setminus A)\)
Интуитивное понимание
Интуитивно симметрическая разность множеств означает выделение уникальных элементов, принадлежащих только одному из множеств. Если A - множество студентов, участвующих в музыкальных кружках, а B - множество студентов, участвующих в спортивных кружках, то симметрическая разность A и B даст множество студентов, участвующих только в одном из кружков.
Примеры применения
Теория Множеств: cимметрическая разность используется для выделения элементов, уникальных для каждого из множеств, исключая общие элементы.
Криптография: в криптографии симметрическая разность может быть использована для создания ключей шифрования.
Исследование данных: в анализе данных симметрическая разность может помочь выявить различия между двумя наборами данных.
Свойства симметрической разности множеств
- Коммутативность: \(A \triangle B = B \triangle A\)
- Ассоциативность: \((A \triangle B) \triangle C = A \triangle (B \triangle C)\)
- Идемпотентность: \(A \triangle A = \varnothing\)
- Элемент Нейтральности: \(A \triangle \varnothing = A\)
Комментарии к калькулятору
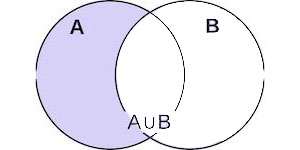
Разностью множества А и В, называется множество, содержащее элементы из множества А, но не входящие в В.
Перейти к расчету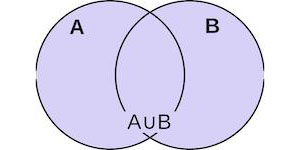
Объединение множеств А и В называется множество А ∪ В, содержащее в себе все элементы исходных множеств.
Перейти к расчету