Калькулятор объема куба

Куб - это одна из самых фундаментальных геометрических фигур, присутствующая как в естественной среде, так и в созданных человеком объектах. Эта простая, но уникальная форма состоит из шести квадратных граней, каждая из которых имеет одинаковый размер и соединяется под прямым углом. Куб можно рассматривать как трехмерное продолжение квадрата в пространстве.
С древних времен куб играл важную роль в математике, архитектуре, искусстве и символизме. В математическом контексте кубы представляют собой идеальный пример для изучения основных понятий стереометрии и геометрических трансформаций. В архитектуре и дизайне кубы часто используются из-за своей простоты, симметрии и универсальности. Они служат основой для создания сложных и функциональных структур. В искусстве и символике куб обычно ассоциируется с устойчивостью, равновесием и идеальной симметрией.
Геометрическое описание куба
Куб – это трехмерная фигура, каждая грань которой представляет собой квадрат. Главные геометрические элементы куба включают грани, ребра и вершины.
Грани:
- Куб имеет шесть граней.
- Каждая грань представляет собой квадрат идентичного размера.
Ребра:
- Куб имеет двенадцать рёбер.
- Все рёбра куба равны по длине.
Вершины:
- Куб имеет восемь вершин.
- В каждой вершине сходятся три ребра.
Геометрические свойства
- Все углы куба прямые (90 градусов).
- Все грани куба - равные квадраты.
- Диагонали всех граней равны и перпендикулярны друг другу.
- Диагональ куба (расстояние между двумя противоположными вершинами) является наибольшей линией, которую можно провести внутри куба.
Таблица характеристик куба
| Характеристика | Описание |
|---|---|
| Грани | 6 квадратов |
| Рёбра | 12, все равной длины |
| Вершины | 8, в каждой сходятся 3 ребра |
| Углы | Прямые (90°) |
| Диагонали граней | Равны и перпендикулярны друг другу |
| Диагональ куба | Наибольшее расстояние внутри куба |
Математические основы расчета
Куб – это трехмерная фигура, у которой все грани являются квадратами. Объем куба рассчитывается с использованием различных математических формул, в зависимости от известных параметров.
Через длину ребра
Объем V куба, если известна длина его ребра \(\ a\), вычисляется по формуле:
Через диагональ стороны
Если известна диагональ стороны куба \(\ d_s\), объем вычисляется так:
Через диагональ куба
При известной диагонали куба \(\ d_c\), объем рассчитывается следующим образом:
Через радиус вписанного шара
Если известен радиус вписанного в куб шара \(\ r_i\), то объем куба находится так:
Через радиус описанного шара
При известном радиусе описанного вокруг куба шара \(\ r_o\), объем куба вычисляется следующим образом:
Эти формулы демонстрируют различные методы расчета объема куба, основываясь на разных исходных данных.
Примеры расчета
- Для куба с длиной ребра 5 м, объем: V = 53 = 125 м3.
- Если диагональ стороны куба равна 7 м, объем: V = (7/√2)3 ≈ 85.85 м3.
- При диагонали куба 10 м, объем: V = (10/√3)3 ≈ 115.47 м3.
- Если радиус вписанного шара 3 м, объем куба: V = (2*3)3 = 216 м3.
- Для куба с радиусом описанного шара 4 м, объем: V = (2*4/√3)3 ≈ 148.15 м3.
Эти примеры демонстрируют, как изменение длины ребра влияет на объем куба.
Заключение
Объем куба – важный геометрический параметр, играющий значительную роль во многих практических и теоретических областях. От архитектуры до логистики, знание того, как рассчитать объем куба, оказывает существенное влияние на решение множества задач. Понимание различных методов расчета объема куба расширяет математические знания и позволяет применять их в различных сферах жизни и профессиональной деятельности.
Комментарии к калькулятору

Калькулятор для подсчета объема груза по количеству коробок или труб разной размерности.
Перейти к расчету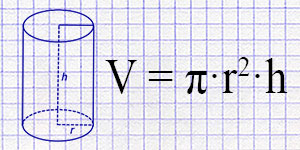
Калькулятор рассчитывает объема цилиндра через высоту и один из параметров: радиус, диаметр или площадь основания.
Перейти к расчету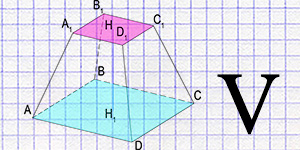
Расчет объема усеченной пирамиды через значения площадей оснований и высоты.
Перейти к расчету