Калькулятор корней
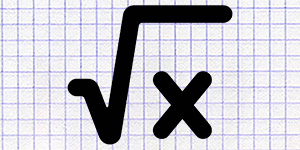
Корень из числа — одно из фундаментальных математических понятий, встречающееся в различных областях науки и инженерии. Это операция, обратная возведению числа в степень, позволяющая определить число, которое, будучи возведенным в определенную степень, дает заданное значение. Наиболее известными являются квадратный и кубический корни, хотя понятие корня может быть расширено до любой степени.
Исторически понятие корня берет свое начало еще в античные времена, когда математики Греции и Вавилона искали методы решения квадратных и кубических уравнений. С развитием математики понятие корня стало применяться всё шире, и на сегодняшний день оно занимает центральное место во многих математических дисциплинах, включая алгебру, геометрию и анализ.
Корень из числа играет ключевую роль не только в теоретической математике, но и в прикладных науках, таких как физика, инженерия и финансы, где он используется для решения широкого спектра задач, от вычисления расстояний и площадей до определения ставок и доходностей. Понимание и умение работать с корнями открывает двери к глубокому анализу и пониманию природы вещей, делая это понятие неотъемлемой частью математического образования и научного исследования.
Основные понятия и определения
Корень n-ой степени из числа \(a\) — это такое число \(b\), которое при возведении в степень \(n\) дает число \(a\). Это понятие записывается как \(b = \sqrt[n]{a}\), где \(n\) — степень корня, а \(a\) — подкоренное число. Для \(n=2\), корень называется квадратным, а для \(n=3\) — кубическим. Понятие корня можно расширить до любого положительного целого числа \(n\).
- Квадратный корень из числа \(a\) — это число \(b\), которое при умножении само на себя дает \(a\). Он обозначается как \(\sqrt{a} = b\).
- Кубический корень из числа \(a\) — это число \(b\), которое при возведении в третью степень дает \(a\). Обозначается как \(\sqrt[3]{a} = b\).
- Положительный и отрицательный корни: Для любого положительного числа \(a\) и четного \(n\) существуют два корня: положительный и отрицательный. Например, \(\sqrt{4}\) может быть как \(2\), так и \(-2\), потому что \(2^2 = 4\) и \((-2)^2 = 4\).
- Иррациональные и рациональные корни: Корень из числа может быть как иррациональным, так и рациональным числом. Например, квадратный корень из \(2\) является иррациональным, а квадратный корень из \(9\) — рациональным (\(3\)).
- Алгебраические свойства корней: Корни подчиняются ряду алгебраических свойств, включая свойства умножения и деления (например, \(\sqrt{a} \times \sqrt{b} = \sqrt{ab}\) и \(\sqrt{a} / \sqrt{b} = \sqrt{a/b}\)), что позволяет упрощать выражения, содержащие корни.
- Комплексные корни: Для отрицательных чисел в случае четных \(n\) корень определяется в области комплексных чисел, используя мнимую единицу \(i\), где \(i^2 = -1\). Например, \(\sqrt{-4} = 2i\).
Понимание этих основных понятий и определений необходимо для глубокого изучения свойств корней и их применения в различных областях математики и науки.
Свойства корней
Корни чисел обладают рядом свойств, которые позволяют упрощать вычисления и решение математических задач. Понимание этих свойств является ключевым для работы с корнями в алгебре и других разделах математики. Ниже перечислены основные свойства корней:
- Произведение корней: Корень произведения равен произведению корней. То есть, \(\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}\).
- Частное корней: Корень частного равен частному корней. Это означает, что \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\), при условии, что \(b \neq 0\).
- Возведение корня в степень: Возведение корня в степень равно корню из числа, возведенного в эту же степень. Таким образом, \((\sqrt[n]{a})^m = \sqrt[n]{a^m}\).
- Извлечение корня из корня: Извлечение корня из корня можно заменить одним корнем, степень которого равна произведению степеней исходных корней. Пример: \(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}\).
- Рационализация знаменателя: Если в знаменателе дроби находится корень, его можно "рационализировать", умножив числитель и знаменатель на сопряженное выражение для знаменателя, чтобы избавиться от корня в знаменателе.
- Корень из единицы: Корень n-ой степени из 1 равен 1 для любого натурального \(n\), то есть, \(\sqrt[n]{1} = 1\).
- Корни из отрицательных чисел: Для четных \(n\), корень n-ой степени из отрицательного числа не существует в множестве действительных чисел, но существует в множестве комплексных чисел.
Эти свойства широко используются при упрощении выражений, решении уравнений и неравенств, а также при выполнении других математических операций, связанных с корнями.
Методы вычисления корней с примерами формул
Для вычисления корней чисел существуют различные методы, как точные, так и приближенные. Вот как эти методы могут быть применены с использованием конкретных формул:
- Прямое вычисление: Для квадратных корней из полных квадратов, например, \(\sqrt{25} = 5\). Кубические корни из полных кубов могут быть вычислены аналогично, например, \(\sqrt[3]{27} = 3\).
- Использование стандартных формул: Применение свойств корней для упрощения, например, \(\sqrt{a^2} = |a|\) или \(\sqrt[3]{a^3} = a\).
- Метод деления пополам: Не имеет прямой формулы, но используется для уточнения корня путем деления интервала пополам и выбора подинтервала, содержащего корень.
- Метод Ньютона (метод касательных): Итерационная формула \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\), где \(f(x)\) — функция, корень которой мы ищем, а \(f'(x)\) — ее производная.
- Использование калькуляторов и компьютерных программ: Большинство калькуляторов и программ используют встроенные алгоритмы для вычисления корней, точные формулы которых могут отличаться в зависимости от программного обеспечения.
- Графический метод: Не основан на формуле, но позволяет визуально определить приближенное значение корня путем нахождения точек пересечения графика функции с осью абсцисс.
Для каждого из этих методов важно понимать основные принципы и уметь применять соответствующие формулы для нахождения корней чисел. В зависимости от задачи и доступных инструментов может быть выбран наиболее подходящий метод вычисления.
Корень из комплексных чисел
Вычисление корней из комплексных чисел является более сложной задачей, чем извлечение корней из действительных чисел, но оно открывает интересные возможности в комплексном анализе и приложениях. Основная формула для нахождения корней комплексного числа опирается на его полярное представление.
Пусть дано комплексное число \(z = a + bi\), где \(a\) и \(b\) — действительные числа, и \(i\) — мнимая единица. Это число можно представить в полярной форме как \(z = r(\cos \phi + i\sin \phi)\), где \(r = \sqrt{a^2 + b^2}\) — модуль комплексного числа, а \(\phi = \arctan(\frac{b}{a})\) — его аргумент.
Корень \(n\)-й степени из комплексного числа \(z\) определяется формулой Муавра:
\[ z^{1/n} = r^{1/n}(\cos(\frac{\phi + 2k\pi}{n}) + i\sin(\frac{\phi + 2k\pi}{n})) \]
где \(k = 0, 1, 2, ..., n-1\). Эта формула дает \(n\) различных значений корня \(n\)-й степени, что соответствует \(n\) точкам на комплексной плоскости, равномерно распределенным по окружности радиуса \(r^{1/n}\).
Таким образом, извлечение корня из комплексного числа приводит не к одному, а к нескольким возможным результатам, каждый из которых представляет собой вершину правильного \(n\)-угольника, вписанного в окружность на комплексной плоскости. Это явление отражает уникальные свойства комплексных чисел и их корней, позволяя проводить глубокий анализ в различных областях математики и физики.
Понимание корней из комплексных чисел и умение работать с ними открывает двери в мир комплексного анализа, обеспечивая мощный инструмент для решения многих теоретических и прикладных задач.
Распространенные ошибки и заблуждения
При работе с корнями чисел, особенно в начальном изучении математики, легко столкнуться с ошибками и заблуждениями, которые могут ввести в заблуждение или привести к неверным результатам. Рассмотрим наиболее частые из них:
- Извлечение корня из отрицательного числа: Многие ученики и студенты забывают, что в рамках действительных чисел нельзя извлечь корень из отрицательного числа. Это правило является основой до введения комплексных чисел, где корень из отрицательного числа становится возможным.
- Распределительное свойство корня: Частая ошибка — попытка применить распределительное свойство к корням, например, предполагая, что \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). Это неверно, за исключением специальных случаев, когда \(a\) и \(b\) образуют определенные пары чисел.
- Ошибки в операциях с корнями: Ошибки в упрощении выражений с корнями, такие как неправильное применение свойств корней или неверное упрощение сложных радикалов, могут вести к неверным ответам.
- Заблуждение о корнях и степенях: Некоторые учащиеся путают операции извлечения корня и возведения в степень, не понимая, что эти операции являются обратными друг другу.
- Игнорирование комплексных корней: При изучении квадратных уравнений легко предположить, что уравнение не имеет решений, если подкоренное выражение отрицательно. Однако с введением комплексных чисел становится ясно, что корни существуют, но они являются комплексными.
Осознание и понимание этих распространенных ошибок и заблуждений помогает избежать их в будущем и глубже понять концепции, связанные с корнями чисел. Важно постоянно практиковаться и консультироваться с учебными материалами или преподавателями для уточнения сомнений и сложностей в этих темах.
Комментарии к калькулятору
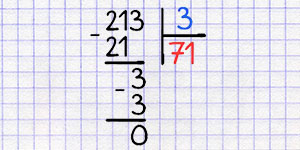
Деление столбиком или уголком поможет разделить многозначные числа за счёт разбивания деления на ряд простых шагов.
Перейти к расчету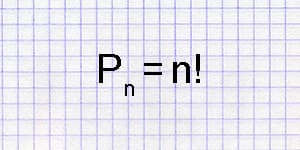
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчету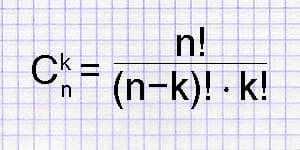
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Перейти к расчету