Калькулятор площади прямоугольника
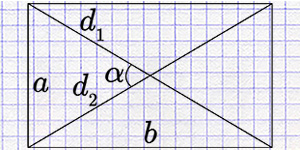
Прямоугольник, одна из наиболее основных геометрических фигур, служит ключевым объектом в изучении площади. Эта фигура, характеризующаяся парой параллельных и равных сторон, представляет собой идеальный пример для объяснения концепции площади, поскольку её можно легко вычислить и представить в виде модели в реальном мире.
Определение и основные свойства прямоугольника
Прямоугольник — это четырехугольник, у которого все углы прямые, то есть равны 90 градусам. Это определение подчеркивает одно из ключевых свойств прямоугольника, делая его важным объектом в геометрии и прикладных областях. Площадь прямоугольника вычисляется по формуле \(S = a \times b\), где \(a\) и \(b\) — длины сторон прямоугольника.
Основные свойства прямоугольника включают:
- Все углы равны 90 градусов, что делает его прямоугольником.
- Противоположные стороны равны и параллельны между собой.
- Диагонали прямоугольника равны и пересекаются, делящись пополам.
- Прямоугольник можно рассматривать как частный случай параллелограмма, у которого хотя бы один угол прямой.
Эти основные свойства лежат в основе геометрических характеристик прямоугольника и определяют методы расчета его площади и других параметров, а также позволяют глубже изучить и применить концепции, связанные с прямоугольниками, в различных математических и прикладных задачах.
Формулы площади прямоугольника
Площадь прямоугольника — это мера пространства внутри четырехугольника с прямыми углами. Существует несколько способов расчета площади прямоугольника в зависимости от известных исходных данных.
Две стороны
Если известны длины двух сторон прямоугольника (\(a\) и \(b\)), площадь находится по формуле: \(S = a \times b\)
Диагонали и угол между ними
При известной длине диагоналей (\(d\)) и угле между ними (\(\theta\)), площадь вычисляется как: \(S = \frac{1}{2} \times d^2 \times \sin(\theta)\)
Сторона и диагональ
Если известна длина одной стороны (\(a\)) и диагонали (\(d\)), то вторую сторону можно найти через теорему Пифагора (\(b = \sqrt{d^2 - a^2}\)), а затем площадь: \(S = a \times \sqrt{d^2 - a^2}\)
Сторона и диаметр описанной окружности
Диаметр описанной окружности (\(D\)) связан с длиной диагонали прямоугольника, поскольку диагональ прямоугольника равна диаметру описанной окружности. Зная одну сторону (\(a\)) и \(D\), можно найти площадь как: \(S = a \times \sqrt{D^2 - a^2}\)
Сторона и периметр
Периметр прямоугольника (\(P\)) и одна из сторон (\(a\)) позволяют выразить вторую сторону (\(b\)) как \(b = \frac{P}{2} - a\), после чего площадь находится через: \(S = a \times \left(\frac{P}{2} - a\right)\)
Радиус описанной окружности и угол между диагоналями
Площадь прямоугольника также может быть найдена через радиус описанной окружности (\(R\)) и угол между диагоналями (\(\theta\)), который равен удвоенному углу между стороной прямоугольника и диагональю: \(S = 2R^2 \sin(\theta)\)
Эти формулы демонстрируют разнообразие методов расчета площади прямоугольника, что делает их применимыми в широком спектре задач, от академических до прикладных.
Примеры расчета площади прямоугольника
Для наглядного понимания методов расчета площади прямоугольника представим несколько типовых задач:
- Расчет площади через две стороны
Пусть длины сторон прямоугольника равны 4 м и 6 м. Тогда площадь прямоугольника \(S\) будет равна \(S = a \times b = 4 \times 6 = 24\) кв.м. - Расчет площади через диагональ и угол между диагоналями
Если длина диагонали прямоугольника составляет 10 м, а угол между диагоналями равен 90 градусам (что характерно для прямоугольника), площадь можно найти по формуле \(S = \frac{1}{2} \times d^2 \times \sin(\theta) = \frac{1}{2} \times 10^2 \times \sin(90^\circ) = 50\) кв.м. - Расчет площади через сторону и диагональ
Для прямоугольника со стороной 3 м и диагональю 5 м, вторая сторона будет равна \(b = \sqrt{d^2 - a^2} = \sqrt{5^2 - 3^2} = 4\) м, а площадь \(S = a \times b = 3 \times 4 = 12\) кв.м. - Расчет площади через сторону и диаметр описанной окружности
Если сторона прямоугольника 6 м, а диаметр описанной окружности 10 м (равен длине диагонали), то вторая сторона найдется как \(b = \sqrt{D^2 - a^2} = \sqrt{10^2 - 6^2} = 8\) м, следовательно, \(S = 6 \times 8 = 48\) кв.м. - Расчет площади через сторону и периметр
Если одна сторона прямоугольника равна 7 м, а его периметр 26 м, то вторая сторона будет \(b = \frac{P}{2} - a = \frac{26}{2} - 7 = 6\) м, а площадь \(S = 7 \times 6 = 42\) кв.м. - Расчет площади через радиус описанной окружности и угол между диагоналями
Для прямоугольника с радиусом описанной окружности 5 м и углом между диагоналями 90 градусов, площадь вычисляется как \(S = 2R^2 \sin(\theta) = 2 \times 5^2 \times \sin(90^\circ) = 50\) кв.м.
Эти примеры демонстрируют, как разные исходные данные могут быть использованы для вычисления площади прямоугольника, обеспечивая полезные навыки для решения широкого спектра задач.
Комментарии к калькулятору
Калькулятор расчета площади квадрата по длине стороны, диагонали, радиусу вписанной и описанной окружности.
Перейти к расчету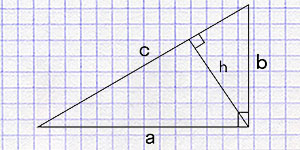
Калькулятор расчета площади прямоугольного треугольника по двум сторонам.
Перейти к расчету