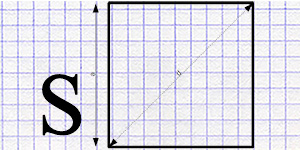
Площадь квадрата
Квадрат — это четырехугольник, обладающий рядом уникальных характеристик, делающих его одной из наиболее изучаемых и применяемых геометрических фигур. Определяется квадрат как правильный многоугольник с четырьмя равными сторонами и четырьмя углами по 90 градусов каждый. Это определение подчеркивает два основных свойства квадрата: равенство всех его сторон и прямые углы.
Свойства квадрата делают его объектом с высокой степенью симметрии. Квадрат обладает несколькими видами симметрии: осевой симметрией относительно своих диагоналей, которые также равны между собой и пересекаются под углом в 90 градусов в центре фигуры, и центральной симметрией относительно точки пересечения диагоналей. Кроме того, квадрат можно описать вокруг окружности и вписать в окружность, что делает его единственным прямоугольником с таким свойством.
Эти основные свойства квадрата лежат в основе его геометрических характеристик и определяют методы расчета площади и других параметров. Понимание этих свойств позволяет глубже изучить и применить концепции, связанные с квадратами, в различных математических и прикладных задачах.
Формула площади квадрата
Площадь квадрата — это мера пространства, ограниченного его сторонами. Существует несколько способов расчета площади квадрата, зависящих от имеющихся данных: длины стороны, длины диагонали, радиуса вписанной или описанной окружности.
1. Через сторону квадрата (\(a\))
Площадь квадрата можно вычислить, если известна длина его стороны. Формула площади квадрата через сторону выражается как:
\[S = a^2\]
где \(S\) — площадь квадрата, \(a\) — длина стороны квадрата.
2. Через диагональ квадрата (\(d\))
Если известна длина диагонали квадрата, площадь можно найти, используя следующую формулу:
\[S = \frac{d^2}{2}\]
Эта формула основана на теореме Пифагора, где диагональ делит квадрат на два равнобедренных прямоугольных треугольника, и длина диагонали является гипотенузой этих треугольников.
3. Через радиус вписанной окружности (\(r\))
Радиус вписанной окружности связан с площадью квадрата следующим образом:
\[S = 4r^2\]
Это вытекает из того, что радиус вписанной окружности равен половине длины стороны квадрата.
4. Через радиус описанной окружности (\(R\))
Площадь квадрата также может быть вычислена через радиус описанной окружности:
\[S = 2R^2\]
Эта формула основывается на связи между радиусом описанной окружности и длиной диагонали квадрата, где \(R\) равен половине длины диагонали.
Каждый из этих способов позволяет найти площадь квадрата в зависимости от исходных данных, предоставляя гибкость при решении геометрических задач.
Примеры расчета площади квадрата
Для лучшего понимания применения формул площади квадрата, рассмотрим несколько практических примеров:
1. Расчет площади через длину стороны
Предположим, длина стороны квадрата \(a\) равна 5 метрам. Используя формулу \(S = a^2\), получаем площадь квадрата:
\[S = 5^2 = 25\ \text{м}^2\]
Таким образом, площадь квадрата с стороной 5 метров составляет 25 квадратных метров.
2. Расчет площади через длину диагонали
Если известна длина диагонали квадрата \(d\) и она равна 7 метрам, то площадь квадрата можно найти по формуле \(S = \frac{d^2}{2}\):
\[S = \frac{7^2}{2} = \frac{49}{2} = 24.5\ \text{м}^2\]
Следовательно, квадрат с диагональю 7 метров имеет площадь 24.5 квадратных метров.
3. Расчет площади через радиус вписанной окружности
Допустим, радиус вписанной окружности \(r\) составляет 2 метра. Тогда площадь квадрата вычисляется как \(S = 4r^2\):
\[S = 4 \times 2^2 = 4 \times 4 = 16\ \text{м}^2\]
Так, квадрат с радиусом вписанной окружности 2 метра имеет площадь 16 квадратных метров.
4. Расчет площади через радиус описанной окружности
Если радиус описанной окружности \(R\) равен 4 метрам, площадь квадрата находится по формуле \(S = 2R^2\):
\[S = 2 \times 4^2 = 2 \times 16 = 32\ \text{м}^2\]
Квадрат, описанный вокруг окружности с радиусом 4 метра, имеет площадь 32 квадратных метра.
Эти примеры демонстрируют различные способы расчета площади квадрата, что делает математические формулы универсальными инструментами для решения задач в области геометрии.
Задачи и упражнения для самостоятельного решения
Для закрепления материала и развития навыков решения геометрических задач предлагаем следующие задачи по теме "Площадь квадрата":
1. Основные задачи на расчет площади
- Задача 1: Длина стороны квадрата составляет 6 см. Найдите площадь квадрата.
- Задача 2: Площадь квадрата равна 49 кв.м. Определите длину стороны квадрата.
2. Задачи на расчет площади через диагональ
- Задача 3: Диагональ квадрата равна 10 см. Вычислите площадь квадрата.
- Задача 4: Площадь квадрата составляет 50 кв.см. Найдите длину его диагонали.
3. Задачи на применение радиуса вписанной и описанной окружности
- Задача 5: Радиус вписанной в квадрат окружности составляет 3 см. Найдите площадь квадрата.
- Задача 6: Радиус описанной около квадрата окружности равен \(5\sqrt{2}\) см. Определите площадь квадрата.
4. Задачи повышенной сложности
- Задача 7: Квадрат вписан в круг радиусом 4 см. Найдите площадь квадрата.
- Задача 8: В квадрат со стороной 8 см вписана окружность. Найдите радиус этой окружности и площадь квадрата.
После попыток самостоятельного решения задач проверьте свои ответы, применяя формулы площади квадрата через известные параметры. Это упражнение поможет не только закрепить знания по теме, но и развить умение применять теоретические знания на практике, а также улучшить навыки решения задач.
Комментарии к калькулятору
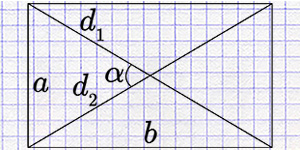
Калькулятор расчета площади прямоугольника по двум сторонам или диагонали и углу.
Перейти к расчету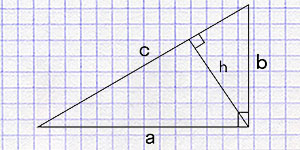
Калькулятор расчета площади прямоугольного треугольника по двум сторонам.
Перейти к расчету