Калькулятор сложения и вычитания дробей
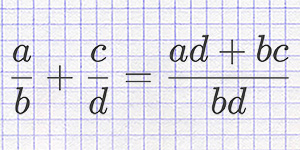
Освоение сложения и вычитания дробей необходимо не только для решения математических задач, но и для развития логического мышления, умения анализировать и синтезировать информацию, что является неотъемлемой частью образовательного процесса в школе и важным навыком в повседневной жизни. Мы рассмотрим различные виды дробей: правильные, неправильные и смешанные, и покажем, как эти знания применяются для выполнения математических операций сложения и вычитания. Это знание откроет перед вами бесконечные возможности для решения широкого спектра задач, от простых арифметических до сложных инженерных расчетов, и поможет улучшить вашу математическую грамотность.
Основы дробей
Основы дробей формируют фундамент для понимания сложения и вычитания дробей, а также других математических операций с ними. Дробь представляет собой часть целого или отношение между двумя числами и состоит из двух компонентов: числителя и знаменателя. Числитель указывает на количество равных частей, а знаменатель — на то, на сколько частей разделено целое. В зависимости от соотношения числителя к знаменателю, дроби бывают правильными, неправильными и смешанными.
- Правильные дроби имеют числитель меньше знаменателя, что означает, что они представляют собой часть, меньшую целого. Пример правильной дроби — \( \frac{3}{4} \).
- Неправильные дроби имеют числитель больше знаменателя или равный ему, что означает, что они представляют собой целое или часть, превышающую целое. Пример неправильной дроби — \( \frac{5}{3} \).
- Смешанные числа состоят из целого числа и правильной дроби, что позволяет представить число более наглядно. Пример смешанного числа — \( 1\frac{2}{3} \).
Для успешного сложения и вычитания дробей важно уметь приводить их к общему знаменателю, что позволяет выполнять операции над дробями с разными знаменателями. Это достигается путем нахождения наименьшего общего знаменателя (НОЗ), который является наименьшим общим кратным знаменателей данных дробей.
Освоение этих основ дробей необходимо для дальнейшего изучения математики и успешного выполнения более сложных задач, включая сложение и вычитание дробей, их умножение и деление, а также применение в практических ситуациях, где требуется работа с частями целого.
Сложение дробей
Сложение дробей — это математическая операция, которая позволяет объединить две или более дробей в одну сумму. Процесс сложения дробей зависит от того, имеют ли дроби одинаковые знаменатели или разные. Для успешного выполнения сложения дробей важно следовать определенным правилам.
Сложение дробей с одинаковыми знаменателями
Сложение дробей с одинаковыми знаменателями является наиболее простым случаем. В этом случае достаточно сложить числители дробей, а знаменатель оставить без изменений. Результатом сложения будет дробь с тем же знаменателем и суммой числителей исходных дробей.
Пример: \( \frac{3}{5} + \frac{2}{5} = \frac{3 + 2}{5} = \frac{5}{5} = 1 \).
Сложение дробей с разными знаменателями
Для сложения дробей с разными знаменателями необходимо привести их к общему знаменателю. Это достигается путем нахождения наименьшего общего знаменателя (НОЗ) для знаменателей исходных дробей и приведения дробей к эквивалентному виду с этим общим знаменателем.
После приведения дробей к общему знаменателю, числители складываются аналогично случаю с одинаковыми знаменателями, а знаменатель остается общим.
Пример: \( \frac{1}{3} + \frac{2}{4} \). НОЗ для 3 и 4 — 12, поэтому приводим дроби к виду \( \frac{4}{12} + \frac{6}{12} = \frac{10}{12} \). Далее, дробь можно сократить, получив \( \frac{5}{6} \).
Практические советы
- Всегда упрощайте дробь до наименьшего возможного выражения после сложения.
- Используйте наименьший общий знаменатель для упрощения вычислений и получения более точного результата.
Сложение дробей требует внимания к деталям и понимания основных принципов работы с дробями. Освоение этих навыков обеспечит успешное выполнение как простых, так и более сложных задач, связанных с дробями.
Вычитание дробей
Вычитание дробей — это процесс, аналогичный сложению, но вместо добавления значений, числители дробей вычитаются друг из друга. Как и в случае со сложением, процесс вычитания зависит от того, одинаковые у дробей знаменатели или разные.
Вычитание дробей с одинаковыми знаменателями
Когда дроби имеют одинаковые знаменатели, вычитание выполняется путем вычитания числителей, а знаменатель остается без изменений. Это простейший случай, который требует минимальных усилий для выполнения.
Пример: \( \frac{5}{7} - \frac{2}{7} = \frac{5 - 2}{7} = \frac{3}{7} \).
Вычитание дробей с разными знаменателями
Для вычитания дробей с различными знаменателями необходимо сначала привести их к общему знаменателю. Этот процесс аналогичен приведению дробей к общему знаменателю при сложении и включает в себя нахождение наименьшего общего знаменателя (НОЗ) для знаменателей обеих дробей.
После того как дроби приведены к общему знаменателю, числители вычитаются друг из друга, а общий знаменатель остается неизменным.
Пример: \( \frac{3}{4} - \frac{1}{6} \). НОЗ для 4 и 6 — 12, поэтому приводим дроби к виду \( \frac{9}{12} - \frac{2}{12} = \frac{7}{12} \).
Практические советы
- Всегда проверяйте, можно ли упростить полученную после вычитания дробь до более простого выражения.
- Используйте наименьший общий знаменатель для упрощения процесса и повышения точности вычислений.
Овладение навыками вычитания дробей облегчит решение множества математических задач и углубит понимание работы с дробными числами. Практика и внимание к деталям помогут успешно справиться с этой задачей.
Упрощение дробей после сложения и вычитания
Упрощение дробей после сложения и вычитания — ключевой шаг, который помогает сделать ответ более понятным и легким для дальнейших расчетов. Этот процесс включает в себя сокращение дроби до ее наименьшего возможного выражения, когда числитель и знаменатель дроби делятся на их общий наибольший делитель (НОД).
Нахождение НОД
Для упрощения дроби необходимо сначала найти наибольший общий делитель числителя и знаменателя. НОД — это наибольшее число, на которое и числитель, и знаменатель могут быть разделены без остатка.
Пример упрощения
Рассмотрим дробь \( \frac{8}{12} \). НОД для 8 и 12 равен 4. Делим числитель и знаменатель на 4, получаем упрощенную дробь \( \frac{2}{3} \).
Почему важно упрощать дроби
- Упрощенные дроби легче понять и использовать в последующих расчетах.
- Это стандартизирует ответы, делая их сравнимыми и удобными для проверки.
- Упрощение дробей помогает визуализировать и анализировать математические модели и уравнения.
Использование упрощенных дробей
После упрощения дроби можно использовать ее в более сложных математических операциях, таких как умножение и деление дробей, а также в задачах на пропорции и проценты. Упрощенная дробь также может служить окончательным ответом, представленным в наиболее компактной и понятной форме.
В заключение, упрощение дробей после сложения и вычитания является неотъемлемой частью работы с дробями, облегчающей понимание и использование математических выражений в различных областях знаний.
Распространенные ошибки при сложении и вычитании дробей
При работе со сложением и вычитанием дробей часто встречаются ошибки, которые могут привести к неправильным результатам. Понимание и избегание этих ошибок поможет улучшить ваши навыки в математике и увеличить точность вычислений.
Игнорирование необходимости общего знаменателя
Одной из самых распространенных ошибок является попытка сложить или вычесть дроби с разными знаменателями без их предварительного приведения к общему знаменателю. Всегда убедитесь, что вы нашли общий знаменатель перед выполнением операции.
Неправильное упрощение дробей
После сложения или вычитания дробей важно правильно упростить полученный результат. Ошибка может заключаться в том, что не находится наибольший общий делитель для числителя и знаменателя, что приводит к ответу, который может быть дальше упрощен.
Неверное сложение числителей и знаменателей
Некоторые учащиеся ошибочно складывают или вычитают числители и знаменатели как отдельные числа, что приводит к неверным результатам. Помните, что операции сложения и вычитания проводятся только с числителями, в то время как знаменатель остается общим для результата.
Забывание о необходимости сокращения дробей
После получения ответа важно проверить, можно ли дробь дальше упростить. Пропуск этого шага оставляет ответ в неупрощенном виде, что может быть не так легко интерпретировать или использовать в дальнейших расчетах.
Ошибки в вычислениях
Простые арифметические ошибки в расчетах числителя или знаменателя могут привести к неправильному итоговому результату. Всегда полезно дважды проверить свои вычисления.
Избегание этих распространенных ошибок требует практики и внимательности. С течением времени и опыта вы будете быстрее замечать и исправлять эти ошибки, улучшая свои навыки работы с дробями.
Комментарии к калькулятору

Калькулятор сложения целых чисел столбиком по школьным правилам. Пошаговые вычисления для проверки расчетов.
Перейти к расчету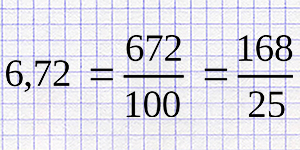
Перевод десятичной дроби в обыкновенную с сокращением числителя и знаменателя.
Перейти к расчету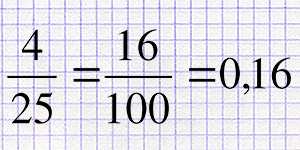
Перевод обыкновенной дроби в десятичную с решением для бесконечных и конечных дробей.
Перейти к расчету