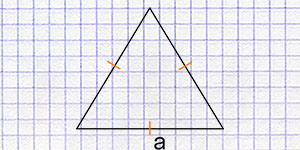
Калькулятор площади равнобедренного треугольника
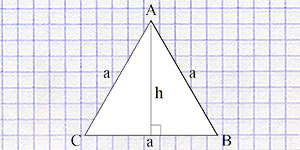
Равнобедренный треугольник имеет две равные стороны (боковые стороны) и, как следствие, два равных угла при основании. Высота равнобедренного треугольника является перпендикуляром, опущенным из вершины, противоположной равным сторонам, на эти стороны.
Методы расчета площади
Выбор метода расчета площади равнобедренного треугольника зависит от того, какие данные у вас имеются.
- С использованием боковой стороны и высоты. Площадь равнобедренного треугольника можно вычислить, зная длину боковой стороны и проведенную к ней высоту. Формула для этого метода: \[ S = \frac{1}{2} \times a \times h. \]
- С использованием длин сторон и основания. Формула для этого метода выглядит следующим образом: \[ S = \frac{1}{4} \sqrt{4a^2 - b^2} \] Этот метод основан на том, что площадь равнобедренного треугольника можно выразить через длину стороны и длину биссектрисы.
- С использованием длин двух сторон и угла между ними. Если известны длины двух равных сторон и угол между ними \( \alpha \), площадь можно вычислить по формуле: \[ S = \frac{1}{2} \times a^2 \times \sin(\alpha). \]
- С использованием длины основания и угла к биссектрисе. Для треугольника с длиной основания \(b\) и углом к биссектрисе \(\alpha\) площадь можно рассчитать по формуле: \( \alpha \), площадь можно вычислить по формуле: \[ S = \frac{1}{2} \cdot b^2 \cdot \tan\left(\frac{\alpha}{2}\right) \]
- С использованием полупериметра и радиуса вписанной окружности. Площадь можно выразить через полупериметр \( p \) и радиус вписанной окружности \( r \): \[ S = p \times r. \]
Пример расчета
Допустим, у нас есть равнобедренный треугольник с боковой стороной \( a = 8 \) и высотой \( h = 6 \). Применим формулу:
\[ S = \frac{1}{2} \times 8 \times 6 = 24 \, \text{кв. ед.} \]
Таким образом, площадь данного треугольника составляет 24 квадратные единицы.
Понимание методов расчета площади равнобедренного треугольника позволяет эффективно работать с этим классом фигур в геометрии. Учитывайте особенности каждого метода и выбирайте наиболее подходящий в зависимости от известных параметров треугольника.
Комментарии к калькулятору
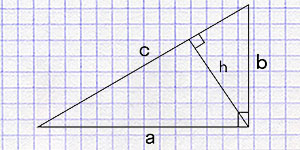
Калькулятор расчета площади прямоугольного треугольника по двум сторонам.
Перейти к расчету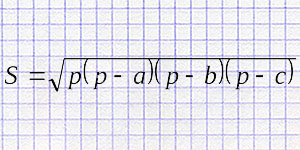
Нахождение площади треугольника по трем его сторонам и полупериметру по формуле Герона.
Перейти к расчету