Формула Бернулли

Формула Бернулли применяется к биномиальным вероятностным распределениям, где есть два возможных исхода (обычно обозначаемых как "успех" и "неудача"). Рассмотрим случай независимых испытаний с фиксированным успехом в каждом испытании и вероятностью успеха .
Теорема Бернулли
Теорема Бернулли формулирует вероятность того, что в серии независимых биномиальных испытаний число успехов равно k. Формулировка теоремы:
Pn(k) = C
Где:
- Pn(k) - вероятность получить успехов в испытаниях,
- C
k n - p - вероятность успеха в одном испытании,
- (1-p) - вероятность неудачи в одном испытании,
- k - количество успехов.
Теорема Бернулли полезна при оценке вероятности успешного исхода в серии независимых событий.
Пример использования
Представим, что у нас есть монета, и мы бросаем ее 10 раз. Каждый раз у нас есть вероятность 0,5 получить "орла". Мы можем использовать формулу Бернулли для определения вероятности получить, скажем, ровно 7 "орлов" в 10 бросках.
Pn(k) = C
Расчет этой формулы даст нам искомую вероятность.
Формула Бернулли - это мощный инструмент для анализа биномиальных вероятностей. Она нашла широкое применение в статистике, физике и других областях. Понимание и умение использовать эту формулу помогут в решении различных задач, связанных с вероятностями успеха и неудачи в серии независимых испытаний.
Комментарии к калькулятору
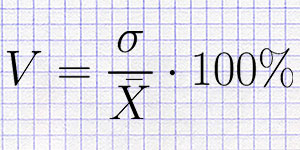
Коэффициент вариации – отношение среднеквадратичного отклонения случайной величины к ее математическому ожиданию.
Перейти к расчету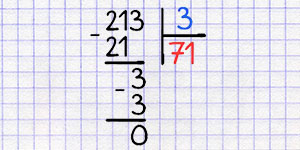
Деление столбиком или уголком поможет разделить многозначные числа за счёт разбивания деления на ряд простых шагов.
Перейти к расчету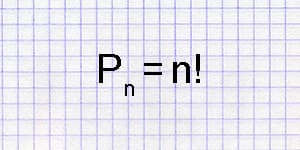
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Перейти к расчету